Question

A current of $0.1{\text{ }}A$. flows through a $25{\text{ }}\Omega$ resistor represented by the circuit diagram. The current in the $80{\text{ }}\Omega$ resistor is

A. $0.1{\text{ }}A\:$
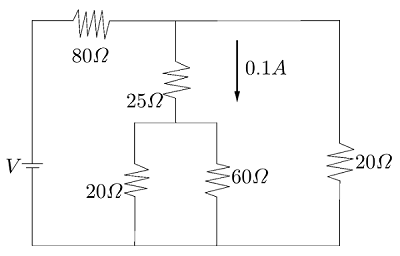
B. $0.2{\text{ }}A\:$
C. $0.3{\text{ }}A\:$
D. $0.4{\text{ }}A\:$

Answer 1

Firstly, we will evaluate the potential of the cell from the given diagram. We will first evaluate the equivalent resistance of the whole circuit and then use ohm's law to evaluate the current through the targeted resistor.

Formulae Used:
${R_{Series}}{\text{ }} = {\text{ }}{R_1}{\text{ }} + {\text{ }}{R_2}{\text{ }} + {\text{ }}...{\text{ }} + {\text{ }}{R_n}$
$\Rightarrow \dfrac{1}{{{R_{Parallel}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}...{\text{ }} + {\text{ }}\dfrac{1}{{{R_n}}}$
$\Rightarrow V{\text{ }} = {\text{ }}IR$
$\Rightarrow I{\text{ }} = {\text{ }}\dfrac{V}{R}$

Complete step by step answer:
In the diagram, it is given that $0.1{\text{ }}A$ of current through the $25{\text{ }}\Omega$ resistor and this resistor lies in an arm parallel to the cell and thus the potential of the cell can be calculated as
$V{\text{ }} = {\text{ }}(0.1{\text{ }}A){\text{ }} \times {\text{ }}(25{\text{ }}\Omega )$
Thus, we get
$V{\text{ }} = {\text{ }}2.5{\text{ }}V$

Now, the net resistance in the secondary circuit in the middle arm can be calculated through the formula of parallel circuits.Thus,
$\dfrac{1}{{{R_{ne{t_{\sec }}}}}}{\text{ }} = {\text{ }}\dfrac{1}{{20}}{\text{ }} + {\text{ }}\dfrac{1}{{60}}{\text{ }} = {\text{ }}\dfrac{1}{{15}}$
Thus,
${R_{ne{t_{\sec }}}}{\text{ }} = {\text{ }}15{\text{ }}\Omega$
Now, for the net resistance in the middle arm, we would use the formula of the series combination.
${R_{Mid}}{\text{ }} = {\text{ }}25{\text{ }} + {\text{ }}15{\text{ }} \\\ \Rightarrow {R_{Mid}}{\text{ }}= {\text{ }}40{\text{ }}\Omega$

Now, we know that current varies inversely with resistance.Let us consider that current $I$ flows out from the cell.Thus,
$\dfrac{{0.1}}{I}{\text{ = }}\dfrac{{20}}{{40}}$
Further, we get
$I{\text{ }} = {\text{ }}0.2{\text{ }}A$
Thus, the current flowing through the targeted resistor is
$0.2{\text{ }} + {\text{ }}0.1{\text{ }} = {\text{ }}0.3{\text{ }}A$

Hence, the correct answer is C.

Note: Students should be very much cautious while evaluating the net resistance as students often make mistakes while judging the type of combination of the resistors. We have used the concept of variance of current with respect to resistance as there are two arms parallel to each other as well as to the arm containing the cell. If we observe carefully, we can see that we have not used the resistance of the resistor in series as it will be of no use if we compare its variance with that of the parallel arm as the potentials are different for both. Thus, students should be considerate while using this process.