Question

A current loop in a magnetic field
A) Experiences a torque whether a field is uniform or non- uniform in all directions
B) Can be in equilibrium in one direction
C) Can be in equilibrium in two orientations, both the states are unstable.
D) Can be in equilibrium in two orientations, one stable while the other is unstable.

Answer 1

Hint: A current-carrying coil will have a magnetic moment associated with it. So the magnetic moment when placed in a magnetic field will experience a torque base on the position of the coil with the field.

Complete step by step answer:

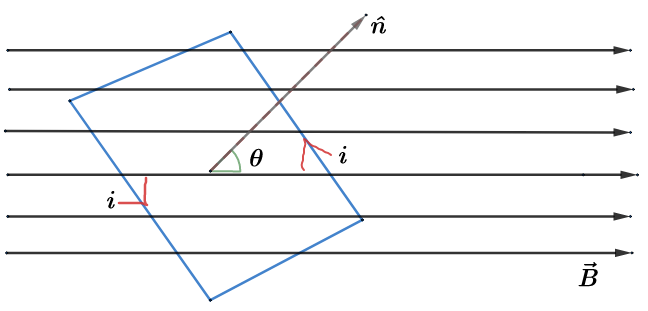
Suppose we have a coil of surface area A which carries a current i. So the magnetic moment associated with the coil is given by, $\text{Magnetic Moment(}\mu \text{)}=i\overrightarrow{\text{A}}$, where $\overrightarrow{\text{A}}$ is the area vector which is perpendicular to the surface area.
So when the coil with a magnetic moment is placed in a magnetic field it experiences a torque which is given by the equation,
Torque$(\tau )=\overrightarrow{\mu }\times \overrightarrow{B}$
Where, the vector B is the magnetic field present. So the torque can be written as,
$\tau =\left( i\overrightarrow{A} \right)\times \overrightarrow{B}=i(\overrightarrow{A}\times \overrightarrow{B})$
Rewriting the cross product in the above equation, we get
$\tau =iAB\sin \theta$
Where, $\text{ }\\!\\!\theta\\!\\!\text{ }$ is the angle between the area vector and the magnetic field.
So if the area vector is parallel to the applied magnetic field, i.e. the angle between A and B is zero. The torque acting on the coil will be zero since $\sin (0)$ is zero. So this can be considered as a stable equilibrium position.
If the area vector is anti-parallel to the applied magnetic field, i.e. the angle between A and B is 180 degrees. The torque acting on the coil will be zero since $\sin (180)$ is zero. So this can be considered as an equilibrium position, but since it is opposite to the direction of the magnetic field. This is a point of unstable equilibrium.
So the answer to the question is option (D)- Can be in equilibrium in two orientations, one stable while the other is unstable.

Note:
Since this torque acts perpendicular to the magnetic moment and the magnetic field, then it can cause the magnetic moment to precess around the magnetic field at a certain frequency called the Larmor frequency.
Magnetic torque on the current-carrying coil is the working principle of electric motors and meters.