Question

A current loop in a magnetic field
A. can be in equilibrium in one orientation.
B. can be in equilibrium in two orientations; both the equilibrium states are unstable.
C. can be in equilibrium in two orientations. One stable while the other is unstable.
D. experiences a torque where the field is uniform or non-uniform in all orientations.

Answer 1

In this question, we need to comment on the current loop which is present in a magnetic field. For this we will use the concept of torque acting on a current-carrying loop suspended in a uniform field. We will establish a relation of the torque for different angles of orientation and find the torque at the desired points.

Complete step by step answer:
As shown in Figure (a), consider a rectangular coil PQRS suspended in a uniform magnetic field $\overrightarrow B$with its axis perpendicular to the field.


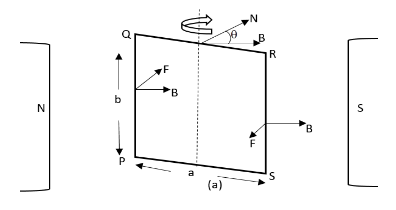
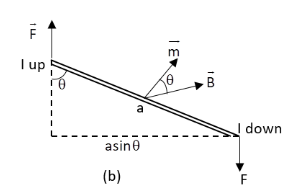
Figure (b) is the top view of the loop; the magnetic dipole moment $\overrightarrow m$ is shown.
Let I$=$current flowing through the coil PQRS
a, b$=$sides of coil PQRS
A$=$ab$=$area of the coil
$\theta =$The angle between the direction $\overrightarrow B$ and normal to the plane of the coil.
According to Fleming’s left-hand rule, the magnetic force on sides PS and QR are equal, opposite, and collinear (along the sides of the loop), so their resultant is zero.
The side PQ experiences a normal inward force equal to, $lbB$ while the side RS experiences an equal normal outward force. These two forces form a couple which exerts a torque given by
$\tau = force \times perpendicular \\\ = lbB \times a\sin \theta \\\ = IBA\sin \theta \\\$
If a rectangular loop has N turns, then $\tau = NIBA\,\sin \theta$
But NIBA$= m,$the magnetic moment of the loop, so $\tau = mb\,\sin \theta$
If $\theta = 0^\circ \Rightarrow \tau = 0$(stable equilibrium)
If $\theta = \pi \Rightarrow \tau = 0$(unstable equilibrium)
So, it does not experience torque in these orientations.
Hence, A current loop in the magnetic field is in equilibrium in two orientations one is stable, and the other is unstable.
Hence, the correct option is (C).

Note: Before applying this concept, we should remember that $\theta$ is the angle between the area vector of the loop and magnetic field, not between the plane of loop and field. Moreover, students should also ensure that the angles are given in the degrees domain and if not then convert it into the same.