Solveeit Logo
Login

Question

Question: A current loop, having two circular arcs joined by two radial lines is shown in the figure. It carri...

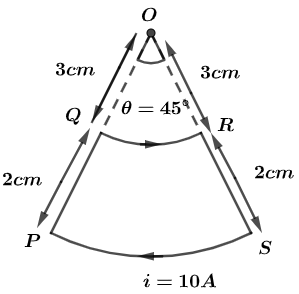
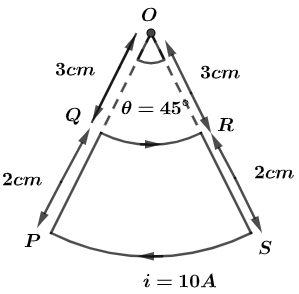
A current loop, having two circular arcs joined by two radial lines is shown in the figure. It carries a current of 10A10A. The magnetic field at the point O will be close to:
A. 1.0×10−5T1.0\times {{10}^{-5}}T
B. 1.5×10−5T1.5\times {{10}^{-5}}T
C. 1.0×10−7T1.0\times {{10}^{-7}}T
D. 2.0×10−7T2.0\times {{10}^{-7}}T

Explanation

Solution

Hint: We know that the formula for magnetic field for an arc subtended by an angle theta can be given by Biot-Savart's law as, B=μ04π⋅θirB=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{\theta i}{r}, using this formula we will find the magnetic field by arc at distance OQ from the centre and then at distance OP from the centre and then we will take their difference to find the over all magnetic field acting at centre O.

Formula used: B=μ04π⋅θirB=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{\theta i}{r}

Complete step by step answer:
In question we have given that a current loop, having two circular arcs joined by two radial lines is shown in the figure and it carries a current of 10A10A.

Now we have been asked to find the magnetic field at centre O, so, now the magnetic field at centre due to circular arc can be given by the formula,
B=μ04π⋅θirB=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{\theta i}{r}
Where, B is magnitude of magnetic field, θ\theta is angle subtended by the arc, r is radius of arc and μ0{{\mu }_{0}} is coefficient of magnetic field.
Now, the arc QR is at the distance OQ from the centre so the radius can be given by,
OQ=r1=3 cm=3×10−2mOQ={{r}_{1}}=3\ cm=3\times {{10}^{-2}}m ………………….(i)
In the same way, arc PS is at distance OP from the centre so, the radius can be given by,
OP=r2=(3+2) cm=5cm=5×10−2mOP={{r}_{2}}=\left( 3+2 \right)\ cm=5cm=5\times {{10}^{-2}}m ……………….(ii)
Now, the magnetic field at centre O by arc QR can be given as,
BOQ=μ04π⋅θir1{{B}_{OQ}}=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{\theta i}{{{r}_{1}}} …………..(iii)
Where,i=10Ai=10A, θ=45∘\theta =45{}^\circ , μ0=4π×10−7{{\mu }_{0}}=4\pi \times {{10}^{-7}} and r1=3×10−2m{{r}_{1}}=3\times {{10}^{-2}}m
Now, we will convert θ\theta from degree to radian using the formula,
rad=deg⁡×π180rad=\deg \times \dfrac{\pi }{180}
⇒rad=45×π180⇒π4rad\Rightarrow rad=45\times \dfrac{\pi }{180}\Rightarrow \dfrac{\pi }{4}rad
Substituting all these values in equation (iii) we will get,
BOP=4π×10−74π×π4×103×10−2{{B}_{OP}}=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\times \dfrac{\pi }{4}\times \dfrac{10}{3\times {{10}^{-2}}} ……………………(iv)
In the same way we can find the magnetic field at centre O by arc PS as,
BPS=μ04π⋅θir2{{B}_{PS}}=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{\theta i}{{{r}_{2}}}
Again, substituting the values we will get,
BPS=4π×10−74π×π4×105×10−2{{B}_{PS}}=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\times \dfrac{\pi }{4}\times \dfrac{10}{5\times {{10}^{-2}}} ………………………(v)
Now, we will consider the directions of current and on the basis of that we will decide the signs, as the currents are in opposite directions to each other it will be a negative sign.
So, the overall magnetic field can be given as,
B=BOP−BPS=4π×10−74π×π4×103×10−2−4π×10−74π×π4×105×10−2B={{B}_{OP}}-{{B}_{PS}}=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\times \dfrac{\pi }{4}\times \dfrac{10}{3\times {{10}^{-2}}}-\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\times \dfrac{\pi }{4}\times \dfrac{10}{5\times {{10}^{-2}}}
Further, simplifying the equation we will get,
⇒B=4π×10−74π×π4×10×[13×10−2−15×10−2]\Rightarrow B=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\times \dfrac{\pi }{4}\times 10\times \left[ \dfrac{1}{3\times {{10}^{-2}}}-\dfrac{1}{5\times {{10}^{-2}}} \right]
⇒B=10−6×π4[5×10−2−3×10−23×10−2×5×10−2]\Rightarrow B={{10}^{-6}}\times \dfrac{\pi }{4}\left[ \dfrac{5\times {{10}^{-2}}-3\times {{10}^{-2}}}{3\times {{10}^{-2}}\times 5\times {{10}^{-2}}} \right]
⇒B=10−6×π4[2×10−215×10−4]\Rightarrow B={{10}^{-6}}\times \dfrac{\pi }{4}\left[ \dfrac{2\times {{10}^{-2}}}{15\times {{10}^{-4}}} \right]
⇒B=10−6×π4[215×10−2]\Rightarrow B={{10}^{-6}}\times \dfrac{\pi }{4}\left[ \dfrac{2}{15\times {{10}^{-2}}} \right]
⇒B=10−6×π4[215×10−2]=10−4×π4[215]\Rightarrow B={{10}^{-6}}\times \dfrac{\pi }{4}\left[ \dfrac{2}{15\times {{10}^{-2}}} \right]={{10}^{-4}}\times \dfrac{\pi }{4}\left[ \dfrac{2}{15} \right]
⇒B=10−4×π3=1×10−5T\Rightarrow B={{10}^{-4}}\times \dfrac{\pi }{3}=1\times {{10}^{-5}}T
Hence, the magnetic field at centre O is 1.0×10−5T1.0\times {{10}^{-5}}T.
Thus, option (a) is correct.

Note: This sum can also be solved directly by using the formula B=μ0θi4π⋅[1r1−1r2]B=\dfrac{{{\mu }_{0}}\theta i}{4\pi }\cdot \left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right] instead of calculating the magnetic fields at r1{{r}_{1}} and r2{{r}_{2}} separately and then find the difference to find the overall magnetic field. Students should also take care of the direction of current flow as considering the directions of flow positive or negative signs are decided.