Question

A current is set up in a long copper pipe. Is there a magnetic field
(a) Inside the pipe
(b) Outside the pipe

Answer 1

The Ampere’s circuital Law gives the relation between the line integral of current and the magnetic field. The answer to the problem requires the application of this law wherein an imaginary closed circular loop is drawn across the material in-order to determine the amount of current produced in the two considered locations of the pipe.

Formula used:
The Ampere’s circuital Law states that:
$\oint {\vec B \cdot d\vec l = {\mu _0}I}$
Where, $\vec B$ is the magnetic field, $d\vec l$ is the length, ${\mu _0}$ is the permittivity constant and $I$ is current in the closed path.

Complete step by step answer:
The problem revolves around the application of the Ampere’s circuital Law because it is a law that relates both quantities, namely, magnetic field and current. The law is used to find out the total amount of current present in a closed circuital path which is produced due to magnetic field or vice versa. The law applied here is the Ampere’s circuital Law because the problem requires to find the magnetic field produced at two different locations with respect to the pipe.

This involves an imaginary path or a closed circuital loop to be drawn around a material across which a current flows which is called the line integral of the current, that is, the total current flowing through a current carrying conductor which in this case is the copper conductor pipe. This closed imaginary surface helps to find out the total current produced in the closed circuit.

Based on this concept let us state the Ampere’s circuital Law. The Ampere’s circuital Law states that the line integral of magnetic field around any closed circuit is equal to the permittivity constant times the total current threading or passing through the closed circuit.The equation from the statement is given by:
$\oint {\vec B \cdot d\vec l = {\mu _0}I}$ -----($1$)
The integral symbol signifies that the integration is done over a closed surface. The law explains that if the magnetic field produced is directed along the tangent at every point in the closed loop and its magnitude is constant then there is a net current that is produced that indicates the total current enclosed in the circular loop. When considering this concept the equation ($1$) becomes:
$BL = {\mu _0}I$ ------($2$)

The long copper pipe is said to have a certain amount of thickness and hence varies from the concept of the law that a current carrying conductor or an infinitely long straight wire is to be considered (since the line integral of the wire is considered as well). Hence, we can say that the copper pipe can be divided into infinitely many straight wires and therefore the application of the law is valid. Here we consider the imaginary loop to be a circle because by definition the magnetic field lines, if present, will be in circles with their centers on the axis of the pipe.

(a) First let us consider a point inside the pipe and if there is a magnetic field produced inside the pipe. Since we are aware that this magnetic field is dependent on the current produced inside the loop as per the law, we first determine the amount of current inside the pipe.
We consider a point inside the pipe and draw an imaginary closed circular path around it with radius lesser than that of cross section of the pipe and apply the Ampere’s circuital Law for the loop. This is shown in the diagram below:

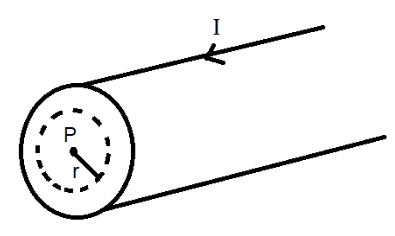
The pipe considered here is assumed to be hollow. Hence, there will be no current flowing inside this loop because the current only flows through a conductor or a conducting wire, that is, current needs a material through which it can travel. Hence the current enclosed inside the circular path will be zero. We now apply the equation ($1$) to determine the magnetic field. From ($1$) we have:
$\oint {\vec B \cdot d\vec l = {\mu _0}I}$
Since, $I = 0$
$\Rightarrow \oint {\vec B \cdot d\vec l = {\mu _0}\left( 0 \right)}$
$\Rightarrow \oint {\vec B \cdot d\vec l = 0}$
$\therefore B = 0$
Hence the magnitude of the magnetic field will also be zero and hence there is no magnetic field inside the pipe.

(b) Now, let us consider the point of the pipe and find out whether there is any field in the outside region with respect to the pipe. We again draw an imaginary closed circular path around it with radius greater than that of cross section of the pipe and apply the Ampere’s circuital Law for the loop. This is shown in the diagram below:

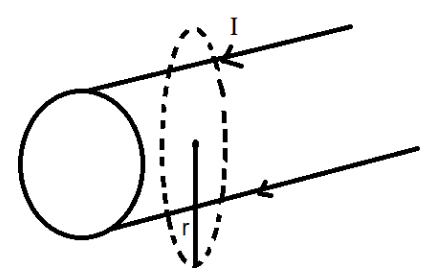
We can clearly see that the circular path considered here includes a part of the whole pipe which has a current flowing through it as given in the question. This current is hence considered in the closed path and this current is given by, let’s say, ${I_{pipe}}$. Now we apply the Ampere’s circuital Law again:
$\oint {\vec B \cdot d\vec l = {\mu _0}I}$
Where, $I$ is the amount current taken into consideration in the closed path. Hence the equation becomes:
$\oint {\vec B \cdot d\vec l = {\mu _0}{I_{pipe}}}$

When we only consider the magnitude of the field which would be constant at all points in the tangent from equation ($2$) the above equation becomes:
$BL = {\mu _0}{I_{pipe}}$
Here the value of $d\vec l$ gives the total integrated length of the path. Since the path considered here is a circle the length is given by the circumference of the circle and let us consider the radius of the closed path to be $r$. Hence the equation becomes:
$B(2\pi r) = {\mu _0}{I_{pipe}}$
$\therefore B = \dfrac{{{\mu _0}{I_{pipe}}}}{{2\pi r}}$
Where ${I_{pipe}}$is the current given to be flowing through the pipe.

Hence this is the magnetic field that is present outside the pipe which is given by the value $\dfrac{{{\mu _0}{I_{pipe}}}}{{2\pi r}}$.

Additional information: Although both Ampere’s law and Biot Savart’s law are similar concept wise the Ampere’s law is said to be more useful under certain conditions. The applications of this law is highly useful as well as it makes it easy to find the magnetic field of a solenoid and a toroid. This law is used for the condition in which a steady current flows through the conductor which does not vary with time.

Note: The Ampere’s circuital Law is similar to Gauss's law in electrostatics where the principle of considering an imaginary surface and finding out the current produced in the surface is the same. The Ampere’s circuital Law is not independent of Biot Savart’s Law and can even be derived from the Biot Savart’s Law. Both of these laws are very useful because both of them relate the magnetic field and the electric current.