Question

A current 'I' is flowing through wire PQR. This wire is bent of an angle and placed on a uniform magnetic field 'B' according to the figure. If PQ=L and angle of PQR =$60^{\circ}$.The ratio of magnetic forces in PQ to QR respectively.

Answer 1

First job is to find out the unknown parameters like length of QR, angle that makes PQ wire with the magnetic field. Use formula for force on a wire and find the force on PQ and QR wire and take the ratio of both the magnetic forces.

Complete answer:
A PQR wire having current ‘I’ is bent as given in the figure below.
Length of PQ is L.

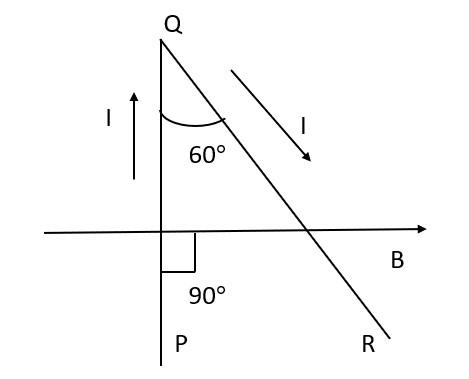
Now we have to find the length of QR.
If we connect P and R then PQR is a right-angled triangle.
$cos60^{\circ} = \dfrac{PQ}{QR}$
$\dfrac{1}{2} = \dfrac{PQ}{QR}$
Given PQ = L
$QR=2L$
Force on a wire is given as-
$F=ILBsin\theta$
Where, F is the magnetic force.
I is the current passing through the wire.
$\theta$ is the angle that current makes with the magnetic field.
L is the length of the wire.
Angle of I and B for wire PQ is $90^{\circ}$.
Magnetic force on PQ wire is –
$F=ILBsin90^{\circ}= ILB$
Angle of I and B for wire PQ is $30 ^{\circ}$.
Magnetic force on QR wire is -
$F=I(2L)Bsin30^{\circ}= ILB$
$\dfrac{F_{PQ}}{F_{QR}} = \dfrac{ILB}{ILB} = 1:1$

Additional Information:
Magnetic force formula-
$F=ILBsin\theta$
From the formula above it is clear that Magnetic force is directly proportional to L, B, I and $\theta$ .
When $\theta = 90^{\circ}$, Force will be maximum on the wire and When $\theta = 0^{\circ}$, Force will be zero on the wire.

Note:
When a wire carries current and is placed in a magnetic field, the wire experiences a force due to the field's interaction and the wire's moving charges. The magnetic force depends on current, length of conductor, magnetic field and the angle between current direction and magnetic field direction.