Question

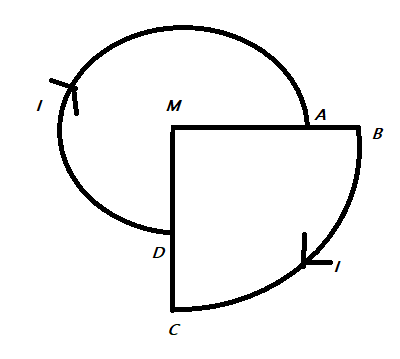
A current $I$ is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is $\dfrac{\mu_{0}I}{R}$ times ($MA=R,MB=2R$ and $\angle DMA=90^{\circ}$).

& A.\dfrac{5}{16}\text{ but out of the plane of the paper} \\\ & \text{B}\text{.}\dfrac{5}{16}\text{ but into the plane of the paper} \\\ & \text{C}\text{.}\dfrac{7}{16}\text{ but out of the plane of the paper} \\\ & \text{D}\text{.}\dfrac{7}{16}\text{ but into the plane of the paper} \\\ \end{aligned}$$

Answer 1

To solve this question we need to make use to the Biot-Savart law, which gives the relation between the current flowing in a conductor and the magnetic it produces. Here we have a combination of two circular wires which carry the current as shown in the figure.

Formula used:
The Biot-Savart law: $dB=\dfrac{\mu_{0}IdLsin\theta}{4\pi r^{2}}$

Complete step by step answer:
We know that the magnetic field is vector thus has it both direction and magnitude .We know that the current carrying conductor produces magnetic field whose direction is given by the right hand thumb rule and the magnitude is given by the Biot-Savart law
Given a combination of curved conductors, the curve $DA$ has radius $R$ while the curve $BC$ has radius $2R$.
Then, we know that the circumference of the circle is given as $2\pi r$, where $r$ is the radius of the circle.
Thus we can say that the total length due to $DA$ as $L_{1}=\dfrac{3}{4}\times 2\pi R=\dfrac{3\pi R}{2}$
Similarly, the total length due to $BC$ as$L_{2}=\dfrac{1}{4}\times 2\pi (2R)=\dfrac{1}{2}\pi (2 R)$

Also we know that $\theta$ is $90^{\circ}$ as the small segment of the wire is perpendicular to the radius.
Substituting the values we get the magnetic field due$DA$ to as$B_{1}=\dfrac{\mu_{0}I}{4\pi R^{2}}\times L_{1}=\dfrac{\mu_{0}I}{4\pi R^{2}}\times\dfrac{3\pi R}{2}=\dfrac{3\mu_{0}I}{8R}$
Similarly, the magnetic field due to $BC$ is given by $B_{2}=\dfrac{\mu_{0}I}{4\pi (2R)^2}\times L_{2}=\dfrac{\mu_{0}I}{4\pi(2 R)^{2}}\times \dfrac{\pi (2R)}{2}=\dfrac{\mu_{0}I}{16R}$
The magnetic field due to $DC$and$AB$ will be $0$ as they are the current and the small segment makes an angle$0^{\circ}$ , then $sin0=0$.
Then the total magnetic field is given as, $B=B_{1}+B_{2}=\dfrac{3\mu_{0}I}{8R}+\dfrac{\mu_{0}I}{16R}=\dfrac{7\mu_{0}I}{16R}$
The direction of the magnetic field is given by right hand thumb rule. Then if we curl the fingers in the direction of the current, then the thumb points the direction of the magnetic field. Here, it points into the paper.
Hence the answer is D.$\dfrac{7}{16}\text{ but into the plane of the paper}$

Note:
Note the fraction of the conductors taken and use the proper radius as given. Be careful with the angle between the current and the small segment of the conductor. Be careful when giving the direction of the magnetic field produced.