Question
Question: A current \[I\] is flowing in a conductor placed along the x-axis as shown in the figure. Find the m...
A current I is flowing in a conductor placed along the x-axis as shown in the figure. Find the magnitude and direction of the magnetic field due to a small current element dl lying at the origin at points (A) (0,d,0) and (B) (0,0,d).
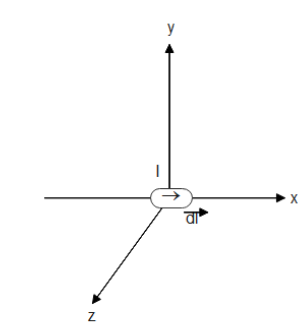
Solution
We need to understand Biot-Savart’s law to find the magnetic field at a certain distance due to a current-carrying conductor. And to find the direction of the field, recall the right-hand thumb rule in which the curl fingers represent the direction of the magnetic field.
Complete step by step answer:
First, let us define Biot-Savart’s law. We know that current flowing through a differential length element dl of a conductor produces a differential magnetic field at a distance say ‘r’ from it. The magnitude of this differential magnetic field is given by Biot-Savart’s law.
According to Biot-Savart’s law, the differential magnetic field db produced by the current in the differential length dl at a point at distance r from the length is proportional to the current in the differential length element, length of the element, sine of the angle between the unit vector of differential element and point P and is inversely proportional to the square of the distance between differential length element and point P.
db=4πμor2Idlsinθ
Where, μo is the permeability of the free space.
Now in the given question dl⊥r , therefore, substituting the values for the point at the x-axis we get
B=4πμod2Idl
And the direction of the field will be in the z-direction which can be found using the right-hand thumb rule. And it will be the same in both cases due to symmetry. And the direction for the point in the z-axis will be negative x-direction.
Note: Biot-Savart’s law can measure the magnetic field due to a current-carrying conductor of any shape. It is not necessary that the conductor has to be straight. We should always use the right-hand thumb rule to find the direction of the magnetic field.
