Question

A current $I$ flows in an infinitely long wire with cross section in the form of a semicircular ring of radius $R$. The magnitude of the magnetic induction at its axis is
$A)\text{ }\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R}$
$B)\text{ }\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}$
$C)\text{ }\dfrac{{{\mu }_{0}}I}{2\pi R}$
$D)\text{ }\dfrac{{{\mu }_{0}}I}{4\pi R}$

Answer 1

We will solve this problem by using the formula for the magnetic field due to an infinitely long current carrying wire. We will consider an infinitely long current carrying wire of infinitesimal thickness in the circumference of the semi-circular ring and then extend it to get the magnetic field due to the current in the whole semicircle.

Formula used:
$dB=\dfrac{{{\mu }_{0}}I}{2\pi R}$

Complete step-by-step answer:
This problem can be solved by finding out the magnetic field due to an infinitely long current carrying wire. The thickness of the wire is an infinitesimal part of the circumference of the semicircular ring and then integrating it for the whole semicircle. Hence, let us proceed to do that.
The magnetic field $dB$ due to an infinitely long wire at a radial distance $R$ from it is given by
$dB=\dfrac{{{\mu }_{0}}I}{2\pi R}$
where ${{\mu }_{0}}=4\pi \times {{10}^{-7}}m.kg.{{s}^{-2}}{{A}^{-2}}$ is the permeability of free space.
Now, let us draw a diagram.

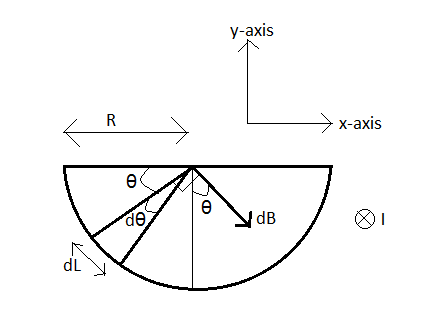
Now the radius of the semicircular ring is $R$.
Therefore the length of its circumference is $L=\pi R$ $\left( \because \text{Circumference of semi circle is }\pi \times \text{Radius} \right)$
Total current in the semicircular ring wire is $I$
As shown in the figure we will take a small thickness element of length $dL$ which carries a current $dI$.
Now, since the wire is uniform we can say that it carries constant current per unit circumference equal to $\lambda$.
$\therefore \lambda =\dfrac{\text{Total current}}{\text{Total circumference}}=\dfrac{I}{\pi R}$ --(2)
Using (2) we get,
$dI=\lambda dL=\dfrac{I}{\pi R}\times dL$ --(3) [Using (2)]
Now, we can see in the figure
$dL=Rd\theta$ --(4)
Hence, putting (4) in (3), we get,
$dI=\dfrac{I}{\pi R}\times Rd\theta =\dfrac{I}{\pi }d\theta$ --(5)
Now, using (1) we get the infinitesimal magnetic field $dB$ at the centre of the ring due to the infinitely long wire with infinitesimal thickness as
$dB=\dfrac{{{\mu }_{0}}dI}{2\pi R}$ --(6)
Putting (5) in (6), we get,
$dB=\dfrac{{{\mu }_{0}}}{2\pi R}\dfrac{I}{\pi }d\theta =\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}d\theta$ --(7)
Now this magnetic field will have two components, one along x-axis and one along y-axis, as shown in the figure.
The y-axis component $d{{B}_{y}}$ is given by
$d{{B}_{y}}=dB\cos \theta$
The x-axis $d{{B}_{x}}$ component is given by
$d{{B}_{x}}=dB\sin \theta$
Now, let us integrate the y-component.
$\int\limits_{0}^{{{B}_{y}}}{d{{B}_{y}}}=\int\limits_{0}^{{{B}_{y}}}{dB\cos \theta }$
Using (7) we get,
$\int\limits_{0}^{{{B}_{y}}}{d{{B}_{y}}}=\int\limits_{0}^{\pi }{\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\cos \theta d\theta =}\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\int\limits_{0}^{\pi }{\cos \theta d\theta }=\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ \sin \theta \right]_{0}^{\pi }=\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ 0-0 \right]=0$ $\left( \because \int{\cos \theta =\sin \theta ,\sin {{0}^{0}}=0,\sin \pi =0} \right)$
$\therefore \left[ {{B}_{y}} \right]_{0}^{{{B}_{y}}}=0$
$\therefore \left[ {{B}_{y}}-0 \right]={{B}_{y}}=0$
Hence, there is no magnetic field component along the y-axis.
Now, let us integrate the y-component.
$\int\limits_{0}^{{{B}_{x}}}{d{{B}_{x}}}=\int\limits_{0}^{{{B}_{x}}}{dB\sin \theta }$
Using (7) we get,
$\begin{aligned} & \int\limits_{0}^{{{B}_{x}}}{d{{B}_{x}}}=\int\limits_{0}^{\pi }{\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\sin \theta d\theta =}\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\int\limits_{0}^{\pi }{\sin \theta d\theta }=\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ -\cos \theta \right]_{0}^{\pi }=\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ -\left( -1 \right)-\left( -\left( 1 \right) \right) \right]=\dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ 1+1 \right]= \\\ & \dfrac{{{\mu }_{0}}I}{2{{\pi }^{2}}R}\left[ 2 \right]=\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R} \\\ \end{aligned}$ $\left( \because \int{\sin \theta =-\cos \theta ,\cos {{0}^{0}}=1,\cos \pi =-1} \right)$
$\therefore \left[ {{B}_{x}} \right]_{0}^{{{B}_{x}}}=\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R}$
$\therefore \left[ {{B}_{x}}-0 \right]={{B}_{x}}=\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R}$
Hence, the magnetic field along the x-axis is $\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R}$.
Therefore, the correct option is $A)\text{ }\dfrac{{{\mu }_{0}}I}{{{\pi }^{2}}R}$.

Note: Sometimes students are not able to catch that they have to use the formula for the magnetic field due to an infinitely long wire and they proceed by using the Biot Savart law for an infinitesimal current element. However, this is not true as the question clearly mentions that the wire is infinitely long and there is no need to use the Biot-Savart’s Law and derive the result for an infinitely long wire or even worse waste time and arrive at the wrong answer. Here in fact we have divided the whole infinitely long wire into thinner infinitely long wires which carry an infinitesimal part of the whole current and integrate the magnetic field due to each of them. This makes the process much simpler.