Question

A current $i$ flows in an infinitely long straight conductor. If $r$ is the perpendicular distance of a point from the lower end of a conductor, then the magnetic induction is given by
(A). $B=\dfrac{{{\mu }_{0}}2i}{4\pi r}$
(B). $B=\dfrac{{{\mu }_{0}}i}{4\pi r}$
(C). $B=\dfrac{{{\mu }_{0}}\pi i}{4\pi r}$
(D). $B=\dfrac{{{\mu }_{0}}2\pi i}{4\pi r}$

Answer 1

The magnetic field due to a straight current carrying conductor depends on the current flowing through the conductor, the distance of the point from the conductor, the angles between the conductor and the lines joining the ends of conductor to the point and the permittivity of space. Substituting corresponding values in the above relation we can calculate the magnetic field.
Formulas used:
$B=\dfrac{{{\mu }_{0}}I}{4\pi r}(\sin {{\theta }_{1}}-\sin {{\theta }_{2}})$

Complete answer:
The magnetic field due to a straight infinitely long current carrying conductor is
$B=\dfrac{{{\mu }_{0}}I}{4\pi r}(\sin {{\theta }_{1}}-\sin {{\theta }_{2}})$
Here, $B$ is the magnetic field
${{\mu }_{0}}$ is the absolute permittivity
$I$ is the current flowing through the conductor
$r$ is the distance between the point and a conductor
${{\theta }_{1}}$ and ${{\theta }_{2}}$ are the angles made by the line joining the point to the ends of the conductor

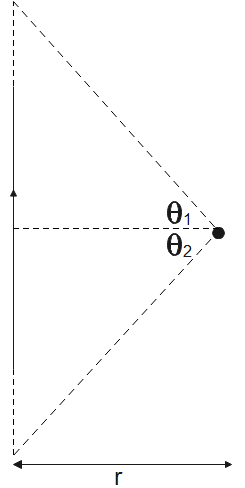
Given that, current flowing through the conductor is $i$, the perpendicular distance between the point and the lower end of the conductor
Since the wire is infinitely long, the lines joining the point to the conductor are almost parallel to the conductor. Therefore,
${{\theta }_{1}}={{90}^{o}}$ and ${{\theta }_{2}}={{0}^{o}}$
We substitute the given values in eq (1),
$\begin{aligned} & B=\dfrac{{{\mu }_{0}}i}{4\pi r}(\sin 90-\sin 0) \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}i}{4\pi r} \\\ \end{aligned}$
Therefore, the magnetic field or magnetic induction due to the conductor is $\dfrac{{{\mu }_{0}}i}{4\pi r}$.

Hence, the correct option is (B).

Note:
It is important to note that the position of the point with respect to the ends of the conductor matter a lot. Since it is infinitely long, the point will be considered to be at the middle of the wire. The direction of the magnetic field is determined by the right hand thumb rule which states that if the thumb represents the direction of current then the curled fingers represent the direction of the magnetic field.