Question
Question: A current I flows in a long thin-walled cylinder of radius R. What pressure does the walls of cylind...
A current I flows in a long thin-walled cylinder of radius R. What pressure does the walls of cylinder experience?
Solution
Express the current density of the current flowing through the cylinder. Determine the expression for the magnetic field at a distance r from the centre of the cylinder due to this current density. We know that the pressure is force per unit area. Express the force on the cylinder due to current density in terms of magnetic field.
Formula used:
The current density J is expressed as,
J=AI
Here, I is the current and A is the area.
F=∫J×BdV
Here, B is the magnetic field.
Complete step by step answer:
We know that the current density of the current flowing through area of cross-section A is given as,
J=AI
Here, I is the current and A is the area.
We assume the thickness of the wall of the cylinder is t. Therefore, the inner and outer radius of the cylinder is as shown in the figure below.
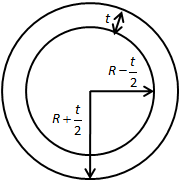
We can calculate the area of the cylinder as follows,
A=(2πR)t
Therefore, the current density becomes,
J=2πRtI …… (1)
We can calculate the value of magnetic field due to current density in the cylinder at a distance r from the centre is,
B(2πr)=2πRtμ0Iπ[r2−(R−2t)2]
⇒B=4πRrtμ0I[r2−(R−2t)2] …… (2)
Now, we have the force due current density acting on the wall of the cylinder is,
F=∫J×BdV
Using equation (1) and (2), we can write the above equation as follows,
F=R−2t∫R+2t8π2R2t2rμ0I2[r2−(R−2t)2]×2πrLdr …… (3)
Here, L is the length of the cylinder.
We know that pressure is a net force divided by area. Therefore, the pressure exerted on the walls of cylinder is,
p=2πRLF
Using equation (3), we can write the above equation as follows,
p=2πRL1R−2t∫R+2t8π2R2t2rμ0I2[r2−(R−2t)2]×2πrLdr
⇒p=8π2R3t2μ0I2R−2t∫R+2t[r2−(R−2t)2]dr
⇒p=8π2R3t2μ0I23(R+2t)3−(R−2t)3−(R−2t)2t
⇒p=8π2R3t2μ0I2(Rt2)
∴p=8π2R2μ0I2
This is the expression for pressure exerted on the walls of the cylinder.
Note:
The integrations used in the above equations are,∫xndx=n+1xn+1+C, where, C is constant of integration which is absent in finite integrations. The formula used to expands the terms in the above calculation is a3−b3=(a−b)(a2+ab+b2).
