Question

A current i flows in a long straight wire with cross-sectional having the form of a thin half-ring radius R (figure shown above). If the induction of the magnetic field at the point O is given as $B=\dfrac{x{{\mu }_{0}}i}{{{\pi }^{2}}R}$. Find x.

Answer 1

Hint: Find the value of the magnitude of magnetic field produced at the point O due the current in the semi circular wire. Use the formula of magnetic field produced at a point that is at a distance of r from a small element of length dl of the wire, i.e.

$dB=\dfrac{{{\mu }_{0}}idl\sin \theta }{4\pi {{r}^{2}}}$.

Formula used:

$dB=\dfrac{{{\mu }_{0}}idl\sin \theta }{4\pi {{r}^{2}}}$

Complete step by step answer:
To find the value of x, let us first find the magnitude of magnetic field (B) created at point O by the current flowing in the wire.

It is given that the current flowing in the wire is I and the radius of the half - ring is R.

Let the direction of the current flowing in the wire be in the clockwise direction.

By using the right hand rule, we get the direction of the magnetic field B into the plane of this page.

Consider a small element of the wire whose length is equal to dl.

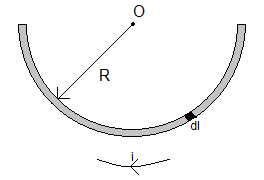
The magnitude of magnetic field at a point due to current carrying element of length dl is given as

$dB=\dfrac{{{\mu }_{0}}idl\sin \theta }{4\pi {{r}^{2}}}$, where r is the distance of the given point from the small element and $\theta$ is the angle between the vectors dl and r.
The direction of dl is always along the direction of the current.

In this case, the value of r is equal to R and since the vector dl is tangent to the semi circle, the radius and dl will be perpendicular. Hence, the value of $\theta =\dfrac{\pi }{2}$.

This given us that $\sin \theta =\sin \dfrac{\pi }{2}=1$

Therefore, the magnitude of the magnitude field due to this small element of the wire is
$dB=\dfrac{{{\mu }_{0}}idl}{4\pi {{R}^{2}}}$

Integrate both the sides, to get the magnitude of B due to the entire semi circular wire.
$\int{dB}=\int{\dfrac{{{\mu }_{0}}idl}{4\pi {{R}^{2}}}}$

Since I and R are constant, we get

$B=\dfrac{{{\mu }_{0}}i}{4\pi {{R}^{2}}}\int{dl}$
$\Rightarrow B=\dfrac{{{\mu }_{0}}i}{4\pi {{R}^{2}}}L$ ……. (ii).

L is the total length of the wire, which is the circumference of the semi circle.

Therefore, $L=\pi R$

Substitute the value of L in equation (ii).

$\Rightarrow B=\dfrac{{{\mu }_{0}}i}{4\pi {{R}^{2}}}.\pi R$
$\Rightarrow B=\dfrac{{{\mu }_{0}}i}{4R}$ ……(iii).

But it is given that that $B=\dfrac{x{{\mu }_{0}}i}{{{\pi }^{2}}R}$

Therefore, $B=\dfrac{x{{\mu }_{0}}i}{{{\pi }^{2}}R}=\dfrac{{{\mu }_{0}}i}{4R}$
$\Rightarrow x=\dfrac{{{\pi }^{2}}}{4}$

Hence the value of x is $\dfrac{{{\pi }^{2}}}{4}$.

Note: The magnitude of the magnetic field produced at the centre of a current carrying ring is equal to $B=\dfrac{{{\mu }_{0}}i}{2R}$. The value of B depends on the current (i) flowing, the distance (r) between the given point (at which B is produced) and the angle between r and dl.

In case of a circular ring (fully or partially), all the factors mentioned above are constant and B will only depend upon the length of the wire.

If half part of the complete circular wire is removed, the contribution of all the small elements of dl length will become of the initial value.

Hence, the value of magnetic field (B’) due to semicircular wire will become half of B.
i.e. $B'=B=\dfrac{1}{2}.\dfrac{{{\mu }_{0}}i}{2R}=\dfrac{{{\mu }_{0}}i}{4R}$.