Question

A current I flows along a round loop. If the integral $\int B.d\vec{r}$ along the axis of the loop within the range from $-\infty$ to $+\infty$ is $= X\mu_0 I$, find $X$.

Answer 1

In order to determine what the coefficient X is, you will need to evaluate the integral mathematically and arrive at the solution to the integral and compare it with the one given in the question and determine X. However, remember that the Ampere’s circuital law relates the magnetic field produced due to a current I in a conducting loop and this is the only result we need to principally determine X.

Formula used:
Magnetic field along the axis produced by a conducting loop of radius R, carrying a current I, at a distance x from the centre of the of the loop :
$B = \dfrac{\mu_0 IR^2}{2(R^2 + x^2)^{3/2}}$, where $\mu_0$ is the magnetic permeability.

Complete answer:
The best way to proceed in the evaluation of this problem is to identify that the setup attributes the Ampere’s circuital law of classical electromagnetism. This law relates the integrated magnetic field around a closed current carrying loop. Note that James Maxwell derived this law, though the name suggests otherwise. Thus, we can derive the magnetic field at a point on the at a point on the axis of the loop and compare it with the one given to us in the question and determine the value of X.

So, we have a circular loop of radius $R$ that carries a current $I$ in the direction as shown in the figure. Let the plane of the loop be perpendicular to the plane of the paper. Now, consider a point lying on the axis(x-axis) of the coil at a distance $x$ from its centre. Therefore, the magnetic field at this point on the axis of the coil is given as:
$B_x = \dfrac{\mu_0 IR^2}{2(R^2 + x^2)^{3/2}}$.

A vector $\vec{r}$ can be defined as the displacement vector from the point P to the point on the axis of the coil that is at a distance $x$ from the centre of the loop
$\vec{r} = \vec{x} + \vec{y} +\vec{z} \Rightarrow dr = dx +dy +dz$ on the elementary scale.
Now, the integral that we need to evaluate is:
$\int_{-\infty}^{+\infty} \vec{B}.d\vec{r}$. But since we have the relation for the magnetic field in the x-direction, this can be rewritten as $\int_{-\infty}^{+\infty} B_xdx$
$\int_{-\infty}^{+\infty} \vec{B}.d\vec{r} = \int_{-\infty}^{+\infty} B_xdx = \int_{-\infty}^{+\infty} \dfrac{\mu_0 IR^2}{2(R^2 + x^2)^{3/2}} . dx = \dfrac{\mu_0 IR^2}{2} \int_{-\infty}^{+\infty} \dfrac{1}{(R^2 + x^2)^{3/2}}dx$

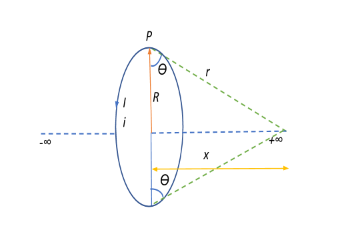
From the diagram, we see that
$tan\theta = \dfrac{x}{R} \Rightarrow x = R tan\theta \Rightarrow dx = R d tan\theta = R sec^2\theta d\theta$
Substituting the dx and x values that we get into the integral and setting the limits from $-\dfrac{\pi}{2}$ to $-\dfrac{\pi}{2}$ which is the plane we are considering, as evident in the diagram.
$\Rightarrow \dfrac{\mu_0 IR^2}{2} \int_{-\pi /2}^{+\pi /2} \dfrac{R\;sec^2\theta\;d\theta }{(R^2 + R^2\;tan^2\theta)^{3/2}} \Rightarrow \dfrac{\mu_0 IR^2}{2} \int_{-\pi /2}^{+\pi /2} \dfrac{R\;sec^2\theta\; d\theta }{(R^2)^{3/2}(1 +tan^2\theta)^{3/2}} \Rightarrow \dfrac{\mu_0 IR^2}{2} \int_{-\pi /2}^{+\pi /2}\dfrac{R\;sec^2\theta\; d\theta }{(R^2)^{3/2}(sec^2\theta)^{3/2}}$
$\Rightarrow \dfrac{\mu_0 IR^2}{2} \int_{-\pi /2}^{+\pi /2}\dfrac{R\;sec^2\theta\; d\theta }{(R^3sec^3\theta)} = \dfrac{\mu_0 IR^2}{2R^2} \int_{-\pi /2}^{+\pi /2} \dfrac{1}{sec\theta}d\theta = \dfrac{\mu_0 I}{2} \int_{-\pi /2}^{+\pi /2} cos\theta\;d\theta$
$\Rightarrow \dfrac{\mu_0 I}{2} \left[sin\theta\right]_{-\pi /2}^{+\pi /2} = \dfrac{\mu_0 I}{2} \left[-sin\left(\dfrac{- \pi}{2}\right) – (-)sin\left(\dfrac{+ \pi}{2}\right)\right] = \dfrac{\mu_0 I}{2} \times 2$
$\Rightarrow \int_{-\infty}^{+\infty} \vec{B}.d\vec{r} = \mu_0 I$
Given in question that $\int_{-\infty}^{+\infty} \vec{B}.d\vec{r} = X\mu_0I$
Comparing our result we get $X=1$.

Note:
Do not forget to alter the integration limits when you change the integrating parameter. Here, we changed our parameter from length or distance to the angle between the point on the loop and the projecting displacement vector.
Also, you can use the right hand thumb rule to determine the direction of the magnetic field produced by the current carrying loop. Make a closed fist but keep your thumb upright, and let the curling of your fingers denote the direction of the current in the loop. Consequently, the direction that your thumb points gives the magnetic field direction.
Additionally, note that Ampere’s circuital law for a current carrying loop given by
$\oint \vec{B}.d\vec{r} = \mu_0 I$ given by the line integral over the closed loop cannot be derived. Its validity is based on the correctness of the results which it predicts.