Question
Question: A current I flow through a closed loop as shown in figure. The magnetic field induction at the centr...
A current I flow through a closed loop as shown in figure. The magnetic field induction at the centre O is:
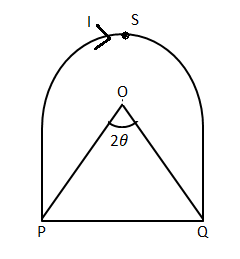
(A)4πRμ0Iθ
(B)4πRμ0I(θ+sinθ)
(C)4πRμ0I(π−θ+sinθ)
(D)4πRμ0I(π−θ+tanθ)
Solution
The relation between current and magnetic field produced by the current is given by the Biot Savart law. Here the current is flowing clockwise. Apply the Biot Savart law on the loop PSR and PQ to obtain the magnetic field of a circle and magnetic field of a segment. Sum of the two magnetic fields gives the resultant magnetic field.
Formula used:
B=2aμ0I
It is the magnetic field of the circle where B is the magnetic field, I is the current.
Complete step to step answer:
The magnetic field produced due to a current carrying segment is given by Biot Savart law. It is a vector quantity. In order to determine the magnetic field produced at a point due to this small element, one can use Biot-Savart’s Law.
Biot-Savart’s law, the magnetic field depends on
Is directly proportional to the current
Is directly proportional to the length
Current is flowing clockwise. Now let us apply the magnetic field due to the loop PSQ. Then magnetic field of a segment is
BPSQ=2Rμ0I(2π2π−2θ)−−−−−(1)
Magnetic field due to the loop PQ. The magnetic field of is
B=2aμ0I(sinθ1+sinθ2)−−−−−(2)
Here a is the perpendicular distance from the point to the wire.
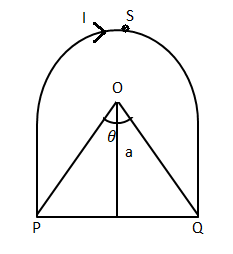
Here a=rcosθ
BPQ=4πRcosθμ0I(2sinθ)
BPQ=4πRμ0I(2tanθ)
BRES=4πRμ0I(2π−2θ)+4πRμ0I(2tanθ)
BRES=4πRμ0I(π−θ+tanθ)
Hence option (D) is the right option.
Note: Biot-Savart’s Law for the magnetic field has certain similarities as well as differences with the coulomb's law. In Biot-Savart’s Law the magnetic field is directly proportional to the sine of the angle. The magnetic field produced due to a current carrying segment is given by Biot Savart law. Biot-Savart’s Law is a vector quantity .
