Question
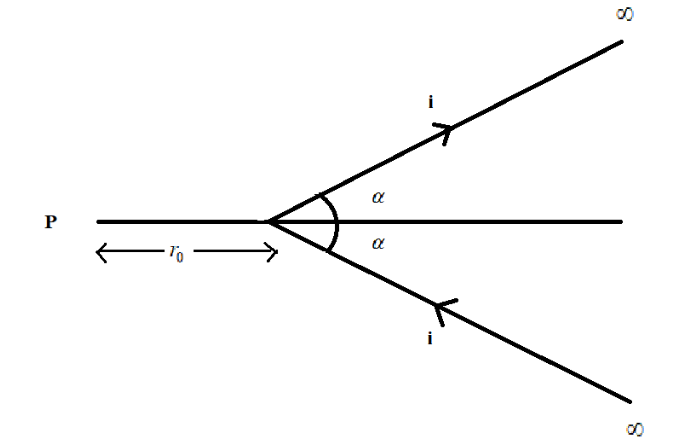
Question: A current carrying wire in the form of ‘V’ alphabet is kept as shown in the figure. Magnetic field i...
A current carrying wire in the form of ‘V’ alphabet is kept as shown in the figure. Magnetic field intensity at point P which lies on the angular bisector of V is
(A) 4πr0μ0i[1−cosα]
(B) 2πr0μ0i[1−cosα]
(C) 4πr0μ0isinα[1−cosα]
(D) 2πr0μ0isinα[1−cosα]
Solution
Magnetic field intensity refers to the ratio of MMFwhich is required for creating a specific Flux Density within a specific material per unit length of that material. The above problem can be solved with the help of Biot-Savart Law.
Formula Used:
B=4πdμ0i(sinθ1−sinθ2)
Complete step by step answer:
According to the Biot-Savart Law,
the magnetic field created due to a finite current carrying wire at a point distance d away from it is given by
B=4πdμ0i(sinθ1−sinθ2)
Here, θ1 and θ2 are the angles that the line joining end point of the wire to the point from with the line of projection from the point to the wire.
So here, magnetic field created due to each wire can be given by
4πr0μ0i(sin90o−sin(90o−α))
On further simplification, we get the magnetic field as
4πr0uoi(1−cosα)
Therefore, the net magnetic field at point P=2πr0uoi(1−cosα)
So, option D is the correct answer.
Additional Information:
Magnetic field intensity, also called magnetic intensity, is a part of the magnetic field in a material that arises from an external current. The magnetic intensity is measured in units of amperes per meter.
Note: Magnetic field intensity is often called magnetic field strength or magnetic intensity. Students get confused when these terms are mentioned. Also, magnetic field and magnetic flux have different meanings. Magnetic field is the region around the magnet where the moving charge experiences a force. On the other hand, magnetic flux shows the strength of the magnetic lines.
