Question

A current-carrying loop consists of two identical semicircular parts each of radius $R$, one lying the x-y plane and the other in the x-z plane. If the current in the loop is $I$, the resultant magnetic field due to the two semiconductor parts will be at their common center will be
A) $\dfrac{{{\mu _0}I}}{{2\sqrt 2 R}}$
B) $\dfrac{{{\mu _0}I}}{{2R}}$
C) $\dfrac{{{\mu _0}I}}{{4R}}$
D) $\dfrac{{{\mu _0}I}}{{\sqrt 2 R}}$

Answer 1

In this solution, we will first determine the direction of the magnetic field of the two half current loops. Then we will calculate the net magnetic field taking into account the direction of the magnetic field.

Formula used: In this solution, we will use the following formula: Magnetic field due to half-circular loop: $B = \dfrac{{{\mu _0}I}}{{4R}}$ where $I$ is the current in the loop and $R$ is the radius of the circular loop.

Complete step by step answer: In this solution, we will use the following formula:
Magnetic field due to half-circular loop: $B = \dfrac{{{\mu _0}I}}{{4R}}$ where $I$ is the current in the loop and $R$ is the radius of the circular loop.
Complete step by step answer:
Let us start by drawing a diagram of the situation given in the question.

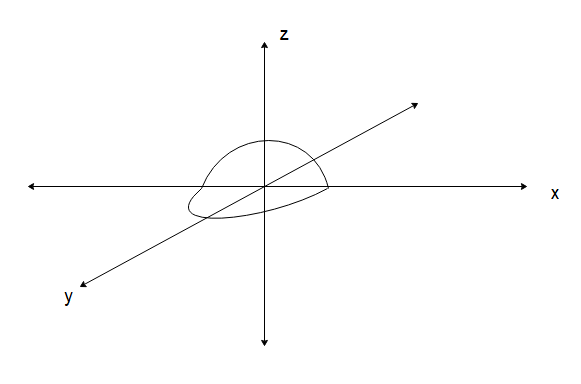
The direction of the magnetic field can be determined by the right-hand rule. For the loop in the x-y plane, the direction of the magnetic field will be in the z-axis. Similarly, the magnetic field due to the loop in the y-z plane will be in the x-direction. Both these magnetic fields will have the same magnitude however their directions will be perpendicular to each other. The magnitude of the magnetic field due to a half current carrying circular coil will be
$B = \dfrac{{{\mu _0}I}}{{4R}}$
So, the net magnetic field at the common centre will the resultant of the two vector magnetic fields which can be calculated as
${B_{net}} = \sqrt {{{\left( {\dfrac{{{\mu _0}I}}{{4R}}} \right)}^2} + {{\left( {\dfrac{{{\mu _0}I}}{{4R}}} \right)}^2}}$
$\Rightarrow {B_{net}} = \sqrt 2 \dfrac{{{\mu _0}I}}{{4R}}$
This can alternatively be written as
${B_{net}} = \dfrac{{{\mu _0}I}}{{2\sqrt 2 R}}$ which corresponds to option (A).

Note: We must be careful to not directly add the magnetic fields of the two current carrying loops as magnetic fields are vector quantities. So, we must take the resultant of the two magnetic fields instead of the algebraic addition of the two quantities.