Question

A cuboidal tank (mass $\approx$ 0) with square cross section has two orifices x and y present on the vertical central line of opposite faces. The tank is completely filled with water and the orifices are just opened. The surface is rough enough to prevent slipping.

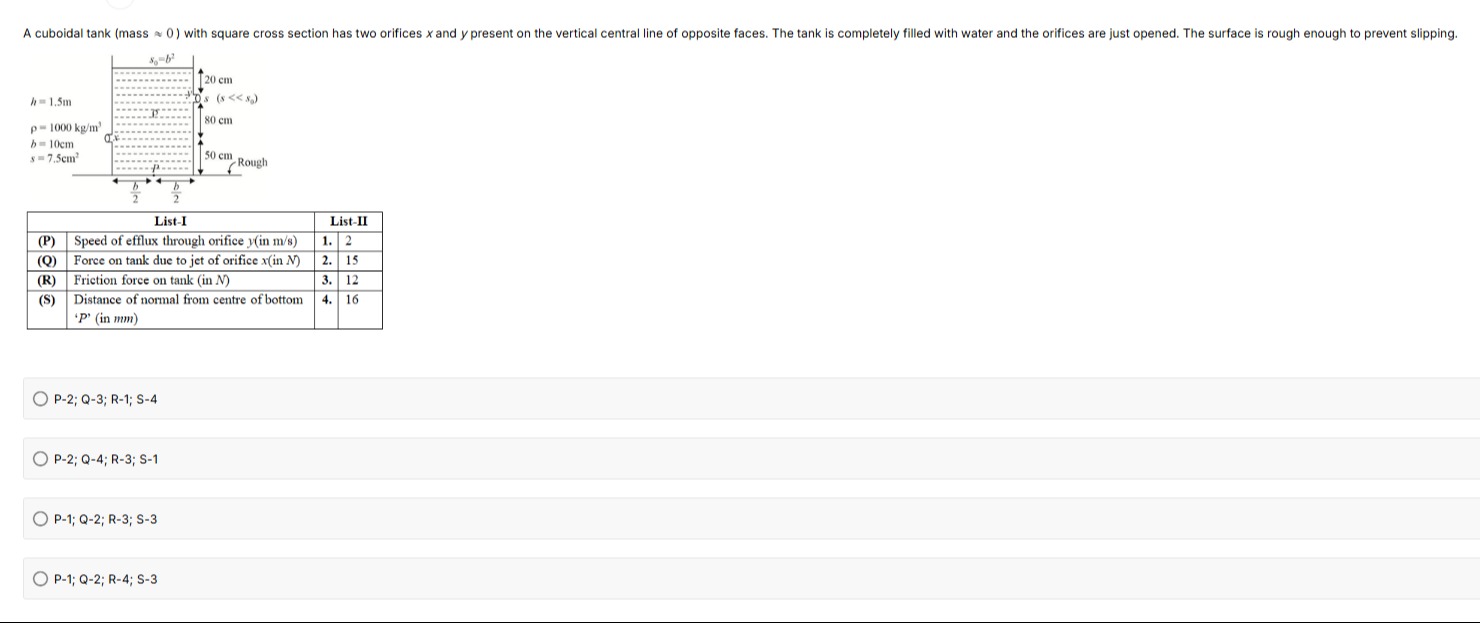
• A. P-2; Q-3; R-1; S-4
• B. P-2; Q-4; R-3; S-1
• C. P-1; Q-2; R-3; S-3
• D. P-1; Q-2; R-3; S-4

Answer 1

Answer: (D)

P–1; Q–2; R–3; S–4

Answer 2

We shall show briefly one acceptable “JEE–NEET” solution. In our analysis one makes the following assumptions:

• The speed from an orifice (with s ≪ s₀) is given by Torricelli’s law. For the orifice on the “y–face” the water‐head is the distance from the free surface to the orifice. Since y is 20 cm below the free surface we get

  $v_y = \sqrt{2g \times 0.20} \approx \sqrt{3.92} \approx 2 m/s$.

• For the lower orifice x the “water‐head” is 1.5 m – (20+80) cm = 1.0 m so that

  $v_x = \sqrt{2 \times 9.8 \times 1.0} \approx 4.43 m/s$.

Then, writing the momentum–flux the force due to the jet emerging at x is

$F_x = \rho \cdot s \cdot v_x^2 \approx 1000 \times (7.5 \times 10^{-4}) \times (4.43^2) \approx 15 N$.

Similarly the jet from y gives a reaction

$F_y = \rho \cdot s \cdot v_y^2 \approx 1000 \times (7.5 \times 10^{-4}) \times (2^2) \approx 3 N$ (more precisely ≃2.94 N).

Thus the net horizontal force on the tank is nearly 15–3 ≃ 12 N. (This is the friction force the rough floor must supply.)

Now, because the two jets act on opposite faces at different vertical levels (x is at 50 cm above the bottom while y is at 1.3 m) they produce a moment on the tank. One may show that in order that the huge weight W (of the contained water, nearly 147 N) produces a counter–moment (via a shift d of the line of action of the normal reaction) one must have

$d = \frac{moment \ due \ to \ jets}{W}$.

A little algebra shows that one obtains d ≃ 16 mm.

Thus the answers come out as:

(P) Speed through y  ≈ 2 m/s   [choose item 1],

(Q) Force on tank due to x ≈ 15 N   [choose item 2],

(R) Friction force on tank ≈ 12 N   [choose item 3],

(S) Shift of normal from P ≈ 16 mm  [choose item 4].

That is, the “correct matching” is:

P–1; Q–2; R–3; S–4.

Explanation (minimal):

1. Use Torricelli’s law for orifice y: $v = \sqrt{2g \times 0.20} \simeq 2 m/s$.
2. For orifice x (water–head = 1.0 m) $v = \sqrt{2g \times 1.0}$ gives $F = \rho \cdot s \cdot v^2 \simeq 15 N$.
3. The net horizontal force (15–3 ≃12 N) is the friction force.
4. Balancing the moment produced by the two jets with the overturning moment of the water weight, the normal force shifts by about 16 mm from the centre P.