Solveeit Logo
Login

Question

Question: A cuboid ABCDEFGH is anisotropic with $\alpha_x = 1 \times 10^{-5} / ^\circ C$, $\alpha_y = 2 \times...

A cuboid ABCDEFGH is anisotropic with αx=1×10−5/∘C\alpha_x = 1 \times 10^{-5} / ^\circ C, αy=2×10−5/∘C\alpha_y = 2 \times 10^{-5} / ^\circ C, αz=3×10−5/∘C\alpha_z = 3 \times 10^{-5} / ^\circ C. Coefficient of superficial expansion of faces can be

A

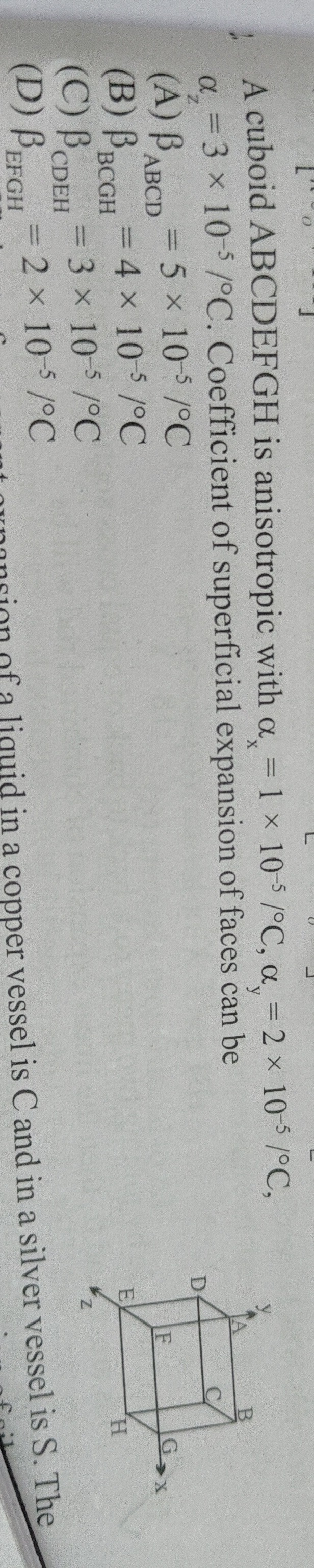
βABCD=5×10−5/∘C\beta_{ABCD} = 5 \times 10^{-5} / ^\circ C

B

βBCGH=4×10−5/∘C\beta_{BCGH} = 4 \times 10^{-5} / ^\circ C

C

βCDEH=3×10−5/∘C\beta_{CDEH} = 3 \times 10^{-5} / ^\circ C

D

βEFGH=2×10−5/∘C\beta_{EFGH} = 2 \times 10^{-5} / ^\circ C

Answer

A, B, C

Explanation

Solution

The coefficient of superficial expansion of a surface is the sum of the coefficients of linear expansion of the two sides forming that surface. For a cuboid with linear expansion coefficients αx\alpha_x, αy\alpha_y, and αz\alpha_z along the x, y, and z directions respectively, the coefficients of superficial expansion for the faces parallel to the coordinate planes are:

  1. Face parallel to the xy-plane (sides along x and y): βxy=αx+αy\beta_{xy} = \alpha_x + \alpha_y
  2. Face parallel to the xz-plane (sides along x and z): βxz=αx+αz\beta_{xz} = \alpha_x + \alpha_z
  3. Face parallel to the yz-plane (sides along y and z): βyz=αy+αz\beta_{yz} = \alpha_y + \alpha_z

Given: αx=1×10−5/∘C\alpha_x = 1 \times 10^{-5} / ^\circ C αy=2×10−5/∘C\alpha_y = 2 \times 10^{-5} / ^\circ C αz=3×10−5/∘C\alpha_z = 3 \times 10^{-5} / ^\circ C

Calculating the possible coefficients of superficial expansion:

  1. βxy=αx+αy=(1×10−5)+(2×10−5)=3×10−5/∘C\beta_{xy} = \alpha_x + \alpha_y = (1 \times 10^{-5}) + (2 \times 10^{-5}) = 3 \times 10^{-5} / ^\circ C.
  2. βxz=αx+αz=(1×10−5)+(3×10−5)=4×10−5/∘C\beta_{xz} = \alpha_x + \alpha_z = (1 \times 10^{-5}) + (3 \times 10^{-5}) = 4 \times 10^{-5} / ^\circ C.
  3. βyz=αy+αz=(2×10−5)+(3×10−5)=5×10−5/∘C\beta_{yz} = \alpha_y + \alpha_z = (2 \times 10^{-5}) + (3 \times 10^{-5}) = 5 \times 10^{-5} / ^\circ C.

Matching these values with the given options: (A) βABCD=5×10−5/∘C\beta_{ABCD} = 5 \times 10^{-5} / ^\circ C. This matches αy+αz\alpha_y + \alpha_z, which is a valid coefficient for a face parallel to the yz-plane. (B) βBCGH=4×10−5/∘C\beta_{BCGH} = 4 \times 10^{-5} / ^\circ C. This matches αx+αz\alpha_x + \alpha_z, which is a valid coefficient for a face parallel to the xz-plane. (C) βCDEH=3×10−5/∘C\beta_{CDEH} = 3 \times 10^{-5} / ^\circ C. This matches αx+αy\alpha_x + \alpha_y, which is a valid coefficient for a face parallel to the xy-plane. (D) βEFGH=2×10−5/∘C\beta_{EFGH} = 2 \times 10^{-5} / ^\circ C. This value does not correspond to any of the possible sums of two linear expansion coefficients.

Therefore, options (A), (B), and (C) represent possible coefficients of superficial expansion for the faces of the cuboid.