Question

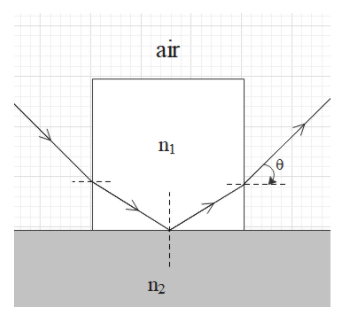
A cubical block of the glass of refractive index ${{n}_{1}}$ is in contact with the surface of the water of refractive index ${{n}_{2}}$. A beam of light is incident on the vertical face of the block (see figure). After refraction, a total internal reflection at the base and refraction at the opposite vertical face, the ray emerges out at an angle $\theta$. The value of $\theta$ is given by

$\text{A}\text{. }\sin \theta$ < $\sqrt{n_{1}^{2}-n_{2}^{2}}$
$\text{B}\text{. tan}\theta$ < $\sqrt{n_{1}^{2}-n_{2}^{2}}$
$\text{C}\text{. }\sin \theta$ < $\dfrac{1}{\sqrt{n_{1}^{2}-n_{2}^{2}}}$
$\text{D}\text{. tan}\theta$ < $\dfrac{1}{\sqrt{n_{1}^{2}-n_{2}^{2}}}$

Answer 1

First find the relation between the refractive indices of the water and the glass mediums with the knowledge that the light suffers total internal reflection when the angle is of incidence at the interface is greater than the critical angle. Then use Snell's law for the refraction at the opposite face of the cube.
Formula used:
${{\theta }_{c}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$
${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$
${{\sin }^{2}}i+{{\cos }^{2}}i=1$

Complete step-by-step solution:
Let us first understand what is meant by a critical angle.
We know that when a ray of light passes from one medium into another medium, the light refracts at the interface at the two mediums.
However, when a ray of light passes from a denser medium into a rarer medium, the light ray may refract or may be reflected into the same medium of incidence. The reflection of light at the interface is called total internal reflection.
Whether the light ray will refract or reflect depends on the angle of incidence. The minimum angle required for total internal reflection is called critical angle.
The critical angle when the light passes from a denser medium of refractive index ${{n}_{1}}$ into rarer medium of refractive index ${{n}_{2}}$ is given as ${{\theta }_{c}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$.
$\Rightarrow \sin {{\theta }_{c}}=\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$

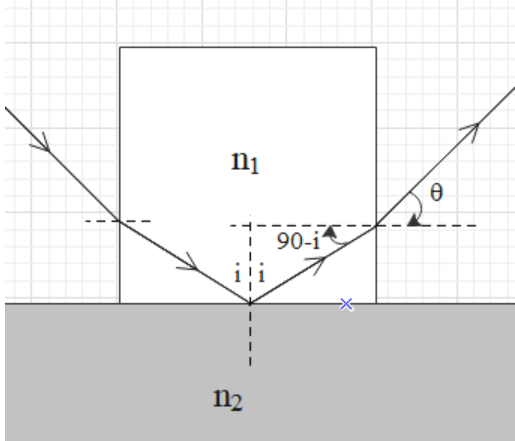
Therefore, the sine of the angle of incidence (i) at the interface of glass-water must be greater than $\dfrac{{{n}_{2}}}{{{n}_{1}}}$.
i.e. sin(i) > $\dfrac{{{n}_{2}}}{{{n}_{1}}}$
Since refractive indices are always positive,
${{\sin }^{2}}i$ > $\dfrac{n_{2}^{2}}{n_{1}^{2}}$
From the figure, we get that the angle of incidence at the opposite face is $\left( {{90}^{\circ }}-i \right)$. And the angle of refraction is r=$\theta$.
From Snell’s law we get that ${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$ …. (ii),
where ${{\mu }_{i}}$ is the refractive index of the medium in which the light is incident, ${{\mu }_{r}}$ is the refractive index of the medium in which the light is refracted.
In this case, ${{\mu }_{i}}={{n}_{1}}$, ${{\mu }_{r}}=1$.
Substitute the values of ${{\mu }_{i}}$, ${{\mu }_{r}}$ and i = $\left( {{90}^{\circ }}-i \right)$ in equation (ii).
$\Rightarrow {{n}_{1}}\sin \left( {{90}^{\circ }}-i \right)=1.\sin \theta$
$\Rightarrow {{n}_{1}}\cos i=\sin \theta$
$\Rightarrow \cos i=\dfrac{\sin \theta }{{{n}_{1}}}$
$\Rightarrow {{\cos }^{2}}i=\dfrac{{{\sin }^{2}}\theta }{n_{1}^{2}}$ …. (iii).
We know that ${{\sin }^{2}}i+{{\cos }^{2}}i=1$.
$\Rightarrow {{\cos }^{2}}i=1-{{\sin }^{2}}i$
Substitute this value in equation (iii).
$\Rightarrow 1-{{\sin }^{2}}i=\dfrac{{{\sin }^{2}}\theta }{n_{1}^{2}}$
$\Rightarrow {{\sin }^{2}}i=1-\dfrac{{{\sin }^{2}}\theta }{n_{1}^{2}}$
We know that ${{\sin }^{2}}i$ > $\dfrac{n_{2}^{2}}{n_{1}^{2}}$.
$\Rightarrow 1-\dfrac{{{\sin }^{2}}\theta }{n_{1}^{2}}$ > $\dfrac{n_{2}^{2}}{n_{1}^{2}}$.
$\Rightarrow \dfrac{n_{1}^{2}-{{\sin }^{2}}\theta }{n_{1}^{2}}$ > $\dfrac{n_{2}^{2}}{n_{1}^{2}}$.
$\Rightarrow n_{1}^{2}-{{\sin }^{2}}\theta$ > $n_{2}^{2}$.
$\Rightarrow {{\sin }^{2}}\theta$ < $n_{1}^{2}-n_{2}^{2}$.
Since refractive indices are always positive and ${{n}_{1}}$ > ${{n}_{2}}$, we can write that
$\sin \theta$ > $n_{1}^{2}-n_{2}^{2}$.
Hence, the correct option is A.

Note: Note the ray of light will suffer total internal reflection at the interface of two mediums only when it passes from a denser medium into a rarer medium.
If the light ray is passing from a rarer medium into denser, it will always refract and bend towards the normal.