Question

A cubical block of side $L$ rests on a rough horizontal surface with a coefficient of friction $\mu$. A horizontal force $F$ is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, find the minimum force required to topple the block.

A) Infinitesimal
B) $\dfrac{{mg}}{4}$
C) $\dfrac{{mg}}{2}$
D) $mg\left( {1 - \mu } \right)$

Answer 1

Here it is mentioned that the block does not slide before toppling. Hence the applied horizontal force is balanced by the frictional force as the block does not slide. Also as the block topples, the line of action of the normal force will shift to the edge O of the block. The torque due to the normal force will be balanced by that due to the applied force and the frictional force. The torque balance equation will help us to derive the minimum force necessary to topple the block.

Formula used:
-The torque acting on a body is given by, $\tau = rF$ where $r$ is the perpendicular distance from the centre of gravity and $F$ is the force acting on the body.

Complete step by step answer.
Step 1: Sketch a figure representing the forces in action as the block topples.

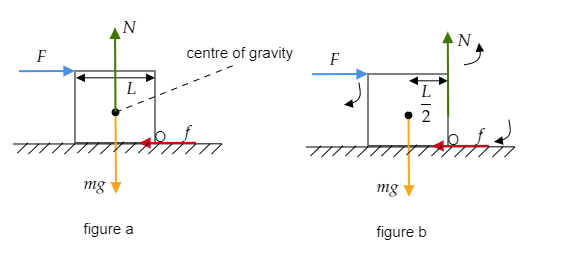
Figure a represents the forces acting on the block before toppling and figure b represents the force acting on the block when it topples.
Here the forces acting on the block are the applied horizontal force $F$, the frictional force $f$, the normal force $N$ and the weight of the block $W = mg$ .
Since no sliding, $F = f$ and also, $N = mg$ .
As the block starts to topple the normal force shifts to the edge O of the block and so the perpendicular distance from the centre of gravity becomes $\dfrac{L}{2}$ as shown in figure b.
Then the torque acting in the clockwise direction will be ${\tau _{clock}} = F\dfrac{L}{2} + f\dfrac{L}{2}$ -------- (1).
The torque acting in the anticlockwise direction will be ${\tau _{anticlock}} = N\dfrac{L}{2}$ --------- (2).
We have to find the minimum applied force for which the block topples.
Step 2: Express the torque balance equation of the block.
The torque balance equation can be expressed as ${\tau _{clock}} = {\tau _{anticlock}}$ -------- (3)
Substituting equations (1) and (2) in equation (3) we get, $F\dfrac{L}{2} + f\dfrac{L}{2} = N\dfrac{L}{2}$
$\Rightarrow F + f = N$
Substituting for $F = f$ and $N = mg$ in the above expression we get, $F + F = mg$
$\Rightarrow F = \dfrac{{mg}}{2}$
$\therefore$ the minimum force required to topple the block will be $F = \dfrac{{mg}}{2}$ .

So the correct option is C.

Note: Here the applied force and the frictional force constitute a couple of equal forces acting in opposite directions and result in a torque in the clockwise direction. The normal force at the edge O of the block and the weight of the block will result in a torque acting in the anticlockwise direction. The perpendicular distance from the centre of gravity of the block for the applied force and the frictional force is also $\dfrac{L}{2}$ as the block is cubical.