Question

A cubical block of side $a$ and density $\rho$ slides over a fixed inclined plane with constant velocity $v$. There is a thin film of viscous fluid of thickness $t$ between the plane and the block. Then the coefficient of viscosity of the thin film will be (acceleration due to gravity is g):

A. $\eta = \dfrac{\rho a g t sin\theta}{v}$
B. $\eta = \dfrac{\rho a g t^2 sin\theta}{v}$
C. $\eta = \dfrac{v}{\rho a g t sin\theta}$
D. None of these

Answer 1

Begin by deducing the influencing forces in this system. In other words, we have a gravitational force and a viscous force acting on the block. Since the block moves with a constant velocity, the net force acting on the block will be zero, implying that the gravitational and viscous forces are equal and opposite to each other.
In such a case, determine the component of the gravitational force that acts along the axis of the viscous force, and equate the two to obtain the necessary relation for the coefficient of viscosity. Remember that the viscous force is described in terms of a velocity gradient over the thickness of the fluid layer.

Formula used:
Gravitational force $F_{g} = mg$
Viscous force $F_{\eta} = \eta A \dfrac{v}{t}$

Complete step-by-step answer:
We are given that the block slides with a constant velocity $v$. This means that the block is not subject to any acceleration and the net force $F_{net}$ acting on the block is zero.
Let the mass of the block be m. $\Rightarrow m_{block} = \rho \times V_{block} = \rho \times a^3$, since the cubical block has a side of length $a$.
Let us now look at the individual forces acting on the block.

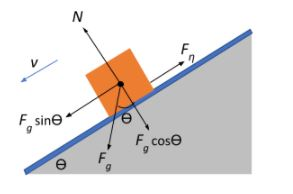
The block is under the influence of two forces that bring about the motion of the block:
Gravitational force $F_{grav}$
The component of the gravitational force acting in the direction of motion of the block is given as:
$F_{grav} = F_g sin\theta = m_{block}gsin\theta = a^3 \rho g sin\theta$
Viscous force $F_{\eta}$
In general, the viscous force offered by the thin layer t of viscous fluid:
$F_{\eta} = \eta A \dfrac{v}{y}$, where $\eta$ is the coefficient of viscosity, A is the area of the surface in contact with the fluid, and the ratio $\dfrac{v}{y}$ is called the velocity gradient

In our case, the viscous force is given as:
$F_{\eta} = \eta (a^2) \dfrac{v}{t}$, where t is the thickness of the viscous fluid layer in contact with a surface area $a^2$ of the cube.
Since $F_{net} = 0$
$\Rightarrow F_{grav} = F_{\eta}$
$\Rightarrow a^3 \rho g sin\theta = \eta (a^2) \dfrac{v}{t}$
$\eta = \dfrac{a \rho g t sin\theta}{v}$
Therefore, the correct option would be: A. $\eta = \dfrac{ \rho a g t sin\theta}{v}$

So, the correct answer is “Option A”.

Note: It is important to understand the nature of viscous force in order to apply it to a numerical analysis. A viscous force is basically a resistance offered by the fluid to any deformation in its structure and orientation. It quantifies an inner frictional force that arises between layers of fluid that are in relative motion.
Note that the ratio $\dfrac{v}{y}$ gives the rate of shear deformation or the rate at which the motion of the body is impeded by a viscous layer of fluid. Thus, the viscous force is a deformative stress response to shear strain between adjacent fluid layers.