Question

A cubical block of side 7 cm is surmounted by a hemisphere of diameter equal to the side of the cube. Find the surface area of the solid.

$$A.{\text{ }}332.5c{m^2} \\\ B.{\text{ }}322.5c{m^2} \\\ C.{\text{ }}342.5c{m^2} \\\ D.{\text{ }}38.5c{m^2} \\\$$

Answer 1

Hint:- Hemisphere is above the cube. We had to only find the curved surface area of the hemisphere and the total surface area of the cube. After that we add both areas and then subtract the area of the hemisphere base from them.

Complete step-by-step answer:

Now let us first draw the figure according to the conditions given in the question.

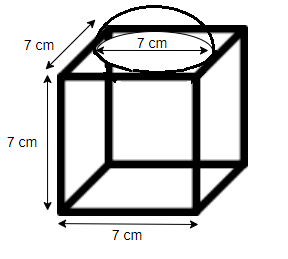
Now as we can see from the above figure that the hemisphere is surmounted by a cube. So, it is clearly obvious that the greatest possible diameter of the hemisphere is equal to the side length of the cube.
So, as given in the question, the diameter of the hemisphere is 7 cm.
Here, we can see from the above figure that the hemisphere falls on the cube. So, in total surface area the base area of the hemisphere should not be included.
So, the surface area of the solid = surface area of cube + curved surface area of the hemisphere – base area of the hemisphere
Now we know that according to the formula for the surface area of the cube which states that if the side length of the cube is a. Then the curved surface area of the cube will be $6{a^2}$.
So, the surface area of the given cube will be = $6{\left( 7 \right)^2} = 6 \times 49 = 294{\text{ }}c{m^2}$
Now according to the formula, the curved surface area of the hemisphere is $2\pi {r^2}$, where r is the radius of the base of the hemisphere.
So, as we know that the diameter of the given hemisphere is 7 cm. So, its radius must be equal to $\dfrac{7}{2}$ cm.
So, the curved surface area of the hemisphere is = $2\pi {\left( {\dfrac{7}{2}} \right)^2} = 2 \times \dfrac{{22}}{7}{\left( {\dfrac{7}{2}} \right)^2} = 11 \times 7 = 77{\text{ }}c{m^2}$
So, now as we know that the base of the hemisphere is of the shape of a circle. And the area of the circle is $\pi {r^2}$, where r is the radius of the circle.
So, the area of base of the hemisphere will be = $\pi {\left( {\dfrac{7}{2}} \right)^2} = \dfrac{{22}}{7} \times \dfrac{7}{2} \times \dfrac{7}{2} = \dfrac{{77}}{2}{\text{ }}c{m^2}$
So, now the surface area of the solid will be = $\left( {294 + 77 - \dfrac{{77}}{2}} \right)c{m^2} = \left( {371 - \dfrac{{77}}{2}} \right)c{m^2}$
Surface area of solid = $\dfrac{{742 - 77}}{2} = 332.5{\text{ }}c{m^2}$
Hence, the correct option will be A.

Note:- Whenever we come up with this type of problem, we should remember that when the hemisphere is surmounted on the cube then the base of the hemisphere is over the surface of the cube. So, the base area of the hemisphere should not be included in the surface area of the solid. So, the surface area of solid will be equal to area of the cube (i.e. $6{a^2}$) + curved surface area of the hemisphere (i.e. $2\pi {r^2}$) – base area of the hemisphere (i.e. $\pi {r^2}$). This will be the easiest and efficient way to find the solution of the problem.