Question

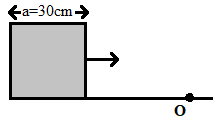
A cubical block of side 30 cm is moving with velocity 2 m/s on a smooth horizontal surface. The surface has a bump at a point ‘O’ as shown in the figure. The angular velocity (in rad/s) of the block immediately after it hits the bump is:

A. 13.3
B. 5.0
C. 9.4
D. 96.7

Answer 1

We are given the side length and velocity of a cubical block moving on a smooth horizontal surface. It is said that the block hits a bump at a point O on the surface. Since there is no external torque at the point O we can say that the angular momentum is conserved. By finding the initial and final angular momenta and equating them, we will get the solution.
Formula used:
${{L}_{i}}=mvr$
${{L}_{f}}=I\omega$

Complete answer:
In the question we are given a cubical block of side 30cm which is moving on a smooth horizontal surface with a velocity 2 m/s.
It is said that there is a bump at the point ‘O’ on the surface.
We know that when the block strikes the bump it will rotate and let ‘$\omega$’ be the angular velocity of the block after it hits the bump.
We know that there is no external torque about the point O. hence we can say that the angular momentum will be conserved, i.e. the initial angular momentum will be equal to the final angular momentum.
$\Rightarrow {{L}_{i}}={{L}_{f}}$, were ‘${{L}_{i}}$’ is the initial angular momentum and ‘${{L}_{f}}$’ is the final angular momentum.
Since the block is moving horizontally on a smooth surface initially, the initial angular momentum is linear angular momentum,
$\Rightarrow {{L}_{i}}=mvr$, where ‘m’ is the mass, ‘v’ is the velocity and ‘r’ is the radius.
In this case we know that the velocity, $v=2m/s$ and we also know that the radius will be half of the side of the block.
Since $a=30cm=0.3m$, $r=\dfrac{0.3}{2}=0.15m$
Therefore we get the initial angular momentum as,
$\Rightarrow {{L}_{i}}=m\left( 2 \right)\left( 0.15 \right)$
$\Rightarrow {{L}_{i}}=0.3m$
Now we need to calculate the final angular momentum. Here we know that the final angular momentum is rotational angular momentum, i.e.
${{L}_{f}}=I\omega$, where ‘$I$’ is the moment of inertia and ‘$\omega$’ is the angular velocity.
The moment of inertia here is the moment of inertia of the block about the point O.

Let us consider the situation when the block hits the bump.

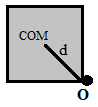
In the figure, ‘COM’ is the centre of mass and ‘d’ is the perpendicular distance from centre of mass to O
By parallel axis theorem we can calculate the moment of inertia about the point O as,
${{I}_{O}}={{I}_{com}}+m{{d}^{2}}$, were ‘${{I}_{com}}$’ is the moment of inertia about the centre of mass and ‘d’ is the perpendicular distance from the centre of mass to the point O.
We know that moment of inertia about centre of mass is given as,
${{I}_{com}}=\dfrac{m{{a}^{2}}}{6}$
We also know that the perpendicular distance from COM to O is half of the diagonal of the block.
We know that the diagonal length is $\sqrt{2}a$, therefore we have
$d=\dfrac{\sqrt{2}a}{2}=\dfrac{a}{\sqrt{2}}$
Hence we can find the moment of inertia about the point O as,
$\Rightarrow {{I}_{O}}=\dfrac{m{{a}^{2}}}{6}+m{{\left( \dfrac{a}{\sqrt{2}} \right)}^{2}}$
$\Rightarrow {{I}_{O}}=\dfrac{m{{a}^{2}}}{6}+\dfrac{m{{a}^{2}}}{2}$
$\Rightarrow {{I}_{O}}=\dfrac{m{{a}^{2}}+3m{{a}^{2}}}{6}$
$\Rightarrow {{I}_{O}}=\dfrac{4m{{a}^{2}}}{6}$
$\Rightarrow {{I}_{O}}=\dfrac{2}{3}m{{a}^{2}}$
Therefore we get the final angular momentum as,
$\Rightarrow {{L}_{f}}=\dfrac{2}{3}m{{a}^{2}}\omega$
Since ${{L}_{i}}={{L}_{f}}$, we can write
$\Rightarrow 0.3m=\dfrac{2}{3}m{{a}^{2}}\omega$
$\Rightarrow 0.3=\dfrac{2}{3}{{a}^{2}}\omega$
We know that $a=0.3m$, therefore,
$\Rightarrow 0.3=\dfrac{2}{3}{{\left( 0.3 \right)}^{2}}\omega$
By solving this we get the angular velocity as,
$\Rightarrow \omega =\dfrac{0.3\times 3}{2\times 0.3\times 0.3}$
$\Rightarrow \omega =\dfrac{3}{2\times 0.3}$
$\Rightarrow \omega =\dfrac{30}{6}$
$\Rightarrow \omega =5rad/s$
Therefore we get the angular velocity as 5 rad/s.

So, the correct answer is “Option A”.

Note:
Angular momentum is the measure of momentum in a rotating body. When there is no external torque acting on the body, then the angular momentum is conserved.
Angular velocity is a vector quantity (a quantity with both magnitude and direction) that measures the rate of change of angular displacement.