Question

A cubical block of mass $M$ is placed at the corner of two inclined planes $A$ and $B$, as shown. Another block of mass $m$ is placed adjacent to $M$, as shown. Let the normal force applied by plane $A$ and $B$ on $M$ be $N_A$ and $N_B$ respectively. Find the value of $m$ in terms of $M$ such that $N_A = N_B$.

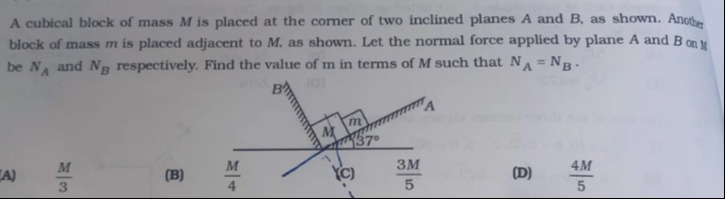
• A. $\displaystyle \frac{M}{3}$
• B. $\displaystyle \frac{M}{4}$
• C. $\displaystyle \frac{3M}{5}$
• D. $\displaystyle \frac{4M}{5}$

Answer 1

Answer: (B)

$\displaystyle \frac{M}{4}$

Answer 2

1. Free-body diagram of block $M$:

• Weight: $Mg$ vertically downward.
• Normal reactions: $N_A$ on the right plane at angle $37^\circ$ to horizontal, and $N_B$ on the left plane (assumed symmetric).
• Additional force from the small block $m$ on plane $A$: this equals the normal force between $m$ and $M$, $N_{m\to M}$.

2. Equilibrium conditions:

• Horizontal equilibrium:

$$N_A\cos 37^\circ + N_{m\to M}\cos(90^\circ-37^\circ) \;=\; N_B\cos 37^\circ$$

• Vertical equilibrium:

$$N_A\sin 37^\circ + N_B\sin 37^\circ + N_{m\to M}\sin(90^\circ-37^\circ) =\; Mg$$

3. Force from block $m$:
Block $m$ on plane $A$ gives $N_{m\to M} = m g \cos37^\circ$.

4. Set $N_A = N_B = N$ and substitute:
From horizontal:

$$N\cos37^\circ + mg\cos37^\circ\cos53^\circ = N\cos37^\circ \;\implies\; mg\cos37^\circ\sin37^\circ = 0$$

(uses $\cos53^\circ=\sin37^\circ$)

From vertical:

$$2N\sin37^\circ + mg\cos37^\circ\sin53^\circ = Mg \;\implies\; 2N\sin37^\circ + mg\cos37^\circ\cos37^\circ = Mg$$

Solving yields

$$m = \frac{M}{4}$$

Key result:

$$\boxed{m = \frac{M}{4}}$$