Question

A cubical block of mass $M$ and edge $a$ slides down a rough inclined plane of inclination with uniform velocity. The torque of the normal force on the block about its center has magnitude

1. Zero
2. $Mga$
3. $Mga\operatorname{Sin} \theta$
4. $\dfrac{{Mga\operatorname{Sin} \theta }}{2}$

Answer 1

Torque is the moment of force. It is the cross product of the force with a perpendicular distance between the axis of rotation and the point of application of force with the force.

Complete step by step solution:
Given that, a cubical block of mass $= m$
And edge length $= a$ ; take $r = \dfrac{a}{2}$
Angle of inclination is $= \theta$
The angle that an inclined plane makes with the horizontal when a body is placed on it is in limiting equilibrium; this angle is called angle of repose.

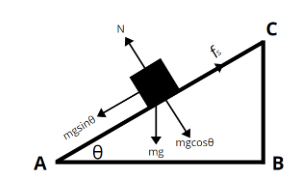
When a cubical block is placed on a rough surface of angle $\theta$ and block slide. Then we have

$F = mg\sin \theta$ …………...(1)

because the force applied is just opposite to the $mg\sin \theta$ similar for normal reaction, When a body is pressed against a surface, the body experiences a force which is perpendicular to the surface.

$N = mg\cos \theta$ ……………..(2)

There are two components, $mg\cos \theta$ and $mg\sin \theta$ but torque is produced only in$mg\sin \theta$ because$mg\cos \theta$ and $N$ pass through the center of the cube, there will be no torque. And

$\overrightarrow \tau = \overrightarrow r \times \overrightarrow F$ ………….(3)
$\tau = rF\sin \theta$

Putting the value of equation (1) in equation (3),
We get,

$\overrightarrow \tau = mg\sin \theta \times \left( {\dfrac{a}{2}} \right)$

Or we can write as,

$\overrightarrow \tau = \dfrac{{mg\sin \theta \times a}}{2}$

Hence, the correct option is (4)

Note: Some point about normal reaction when a block is placed on a table, the normal reaction on the block by the table is $N = mg$ but when block is placed on an inclined plane the normal reaction force, $N = mg\cos \theta$