Solveeit Logo
Login

Question

Question: A cubic polynomial \(f(x) = a{x^3} + b{x^2} + cx + d\) has a graph which is tangent to the x- axis a...

A cubic polynomial f(x)=ax3+bx2+cx+df(x) = a{x^3} + b{x^2} + cx + d has a graph which is tangent to the x- axis at 22 has another x- intercept at −1 - 1 and has y- intercept at −2 - 2 as shown. The values of a+b+c+da + b + c + d is

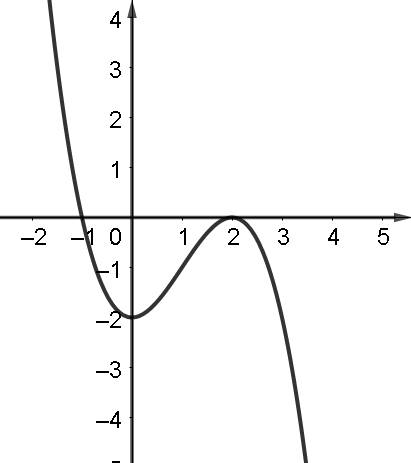
A. −2 - 2
B. −1 - 1
C. 00
D. 11

Explanation

Solution

In this question, we are given a function with unknown constants and their graph. We have to find the values of these constants.
So, we will find the values of the function at different values of xx , then solve them to get the values of a,b,c,da,b,c,d .
The point to remember here is, since, it has a tangent at the x-axis at the point 22 , so, the derivative of this function at the point 22 will be zero.

Complete step-by-step answer:
We are given a function with unknown constants f(x)=ax3+bx2+cx+df(x) = a{x^3} + b{x^2} + cx + d and its graph.
To find the values of aa , bb , cc and dd .
First, we will differentiate the given function and find its value at x=2x = 2 .
On differentiating, we get, f′(x)=3ax2+2bx+cf'(x) = 3a{x^2} + 2bx + c , now, putting x=2x = 2 in it, we get, f′(x)=3a(2)2+2b(2)+cf'(x) = 3a{(2)^2} + 2b(2) + c , i.e., f′(2)=8a+4b+cf'(2) = 8a + 4b + c .
From the graph, it is clear that, f′(2)=0f'(2) = 0 , i.e., 8a+4b+c=08a + 4b + c = 0 … (1)
Also, from the graph, f(2)=0f(2) = 0 , f(−1)=0f( - 1) = 0 and f(0)=−2f(0) = - 2 , so, first putting, x=2x = 2 in the given function f(2)=8a+4b+2c+d=0f(2) = 8a + 4b + 2c + d = 0 , then, putting, x=−1x = - 1 , we get, f(−1)=−a+b−c+d=0f( - 1) = - a + b - c + d = 0 and finally, putting x=0x = 0 , we get, f(0)=d=−2f(0) = d = - 2 .
Now, since we have the value of dd , so we will put it in all equations, then the equation becomes,
f(−1)=−a+b−c=2f( - 1) = - a + b - c = 2
f(2)=8a+4b+2c=2f(2) = 8a + 4b + 2c = 2
f′(2)=8a+4b+c=0f'(2) = 8a + 4b + c = 0
On solving these equations simultaneously, we get, a=−12a = - \dfrac{1}{2} , b=32b = \dfrac{3}{2} , c=0c = 0 and d=−2d = - 2 .
Hence, the value of a+b+c+d=−12+32+0−2a + b + c + d = - \dfrac{1}{2} + \dfrac{3}{2} + 0 - 2 , least common multiple of the denominators is 22 , so we get, a+b+c+d=−1+3+0−42a + b + c + d = \dfrac{{ - 1 + 3 + 0 - 4}}{2} , on simplifying, we get, a+b+c+d=−22=−1a + b + c + d = \dfrac{{ - 2}}{2} = - 1 .

So, the correct answer is “Option B”.

Note: If a function has a tangent at a point x=ax = a , then, it means, it is the critical point of that function and the derivative of the function is zero at that point.
Perform the calculations carefully, to avoid silly mistakes.
One should know how to read a graph to solve such questions.