Question

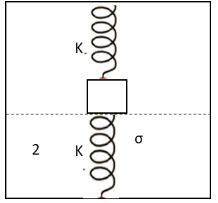
A cubic block of side $a$ is connected with two similar springs as shown. Initially, the bottom surface of the block of density $\sigma$ touches the surface of the fluid of density $2\sigma$ while floating. A weight is placed on the block so that it is immersed half in the fluid, find the weight:

A. $a\left( {\dfrac{K}{2} + {a^2}\sigma g} \right)$
B. $a\left( {K + {a^2}\sigma g} \right)$
C. $a\left( {K + \dfrac{{{a^2}}}{2}\sigma g} \right)$
D. $\dfrac{a}{2}\left( {K + {a^2}\sigma g} \right)$

Answer 1

We can use the formulae for spring force, buoyant force on an object immersed in the liquid, density of an object and net force according to Newton’s second law of motion. First determine weight of the cubical block in terms of its density. Then apply Newton’s second law of motion to the block for the first case in the vertical direction. Then determine the displacement of the springs for the second case and apply Newton’s second law of motion to the block in the vertical direction.

Formulae used:
The spring force ${F_s}$ acting on the spring is given by
${F_s} = kx$ …… (1)
Here, $k$ is the spring constant and $x$ is the displacement of the spring.
The buoyant force ${F_B}$ acting on the object immersed in the fluid is
${F_B} = \rho Vg$ …… (2)
Here, $\rho$ is density of the fluid, $V$ is volume of the immersed object and $g$ is acceleration due to gravity.
The density $\rho$ of an object is
$\rho = \dfrac{m}{V}$ …… (3)
Here, $m$ is the mass of the object and $V$ is the volume of the object.

Complete step by step answer:
We have given that the side of the cubical block is $a$ and the density of the block is $\sigma$. Initially, the lower surface of this block just touches the fluid of density $2\sigma$and then half of this block is immersed in the fluid when a weight is placed on this block.We are asked to calculate the value of this weight.Let $m$ be the mass of the cubical block.Let us first determine weight ${W_b}$ of the cubical block.
${W_b} = mg$
According to equation (3), the above equation becomes
${W_b} = \sigma {a^3}g$
When the cubical block just touches the surface of the fluid, let $x$ be the extension of the upper spring in the downward direction and hence, the compression in the lower spring will be $x$.

According to Newton’s second law of motion, the weight of the cubical block is balanced by the spring force of the two springs.
$\sigma {a^3}g = Kx + Kx$
$\Rightarrow \sigma {a^3}g = 2Kx$
$\Rightarrow x = \dfrac{{{a^3}\sigma g}}{{2K}}$
This is the expression for displacement of the spring.
When half of the cubical the block submerged in the fluid, the extension of the upper spring becomes $x + \dfrac{a}{2}$ and compression in the lower spring becomes $x + \dfrac{a}{2}$.
When the block is half submerged in the fluid, the weight ${W_b}$ of the cubical block and the extra weight $W$ placed on the cubical block are balanced by the spring forces of the two springs and buoyant force ${F_B}$ on the cubical block.
${W_b} + W = 2K\left( {x + \dfrac{a}{2}} \right) + {F_B}$
$\Rightarrow \sigma {a^3}g + W = 2K\left( {\dfrac{{{a^3}\sigma g}}{{2K}} + \dfrac{a}{2}} \right) + 2\sigma \left( {{a^2}\dfrac{a}{2}} \right)g$
$\Rightarrow \sigma {a^3}g + W = {a^3}\sigma g + \dfrac{{2Ka}}{2} + \sigma {a^3}g$
$\Rightarrow W = {a^3}\sigma g + Ka$
$\therefore W = a\left( {K + {a^2}\sigma g} \right)$
Therefore, the weight is $a\left( {K + {a^2}\sigma g} \right)$.

Hence, the correct option is B.

Note: The students should keep in mind that only half of the cubical block is immersed in the fluid. Hence, while determining the buoyant force acting on the cubical block immersed in the fluid, the volume of only half block should be taken. Also, the value of extension of the upper spring is always the same as compression in the lower spring.