Question

A cubic block is floating in a liquid with half of its volume immerases in the liquid. When the whole system accelerates downward with an acceleration $\dfrac{g}{3}$. The fraction of volume immersed in liquid will be
A. $\dfrac{1}{2}$
B. $\dfrac{3}{8}$
C. $\dfrac{2}{3}$
D. $\dfrac{3}{4}$

Answer 1

First we have to draw a free body diagram. Then with the help of that free body diagram equate the buoyancy force due to liquid with the force experienced by the block due to gravity. We will get the relation between the density of two substances. Secondly after applying a downward acceleration on the system we will get a pseudo force, now equating the force that is applied on the system after downward acceleration we will get the fraction of volume immersed in the liquid.

Complete answer:
As per the given problem we know that a cubic block is floating in a liquid with half of its volume immerases in the liquid.Now we need to calculate the fraction of volume immersed when the whole system accelerates downward with an acceleration $\dfrac{g}{3}$.Let us assume the ass of the block be m, the buoyancy force of the liquid be B. Now drawing the free body diagram before the downward acceleration we will get,

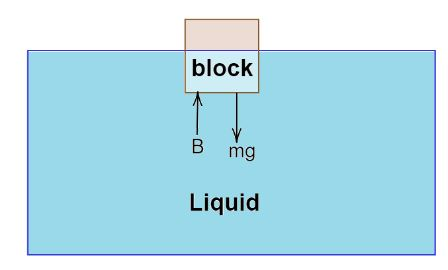
Now from the diagram we can say,
$B = mg$
Where the formula for buoyancy force is,
$B = \rho l\dfrac{V}{2}g$
Where, density of the liquid is $\rho l$ and the volume of the block be $V$ and the buoyancy force is only applied to half of the boluck.

Now equating this above formula with the force due to gravity we will get,
$\rho l\dfrac{V}{2}g = mg$
The mass of the block can also be written as product of density od the block and its volume
$\rho l\dfrac{V}{2}g = \rho bVg$
Now cancelling the common terms we will get,
$\dfrac{{\rho l}}{2} = \rho b \ldots \ldots \left( 1 \right)$
Now when the whole system accelerates downward with an acceleration $\dfrac{g}{3}$ then a pseudo force will be applied on the system.
Here the buoyancy force also changes due to the downward acceleration .
Now the free body diagram will look like,

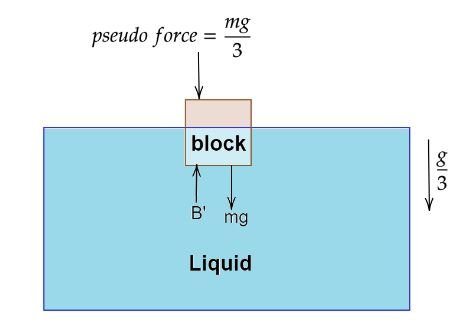
From the above diagram we can say,
$B' = mg + \dfrac{{mg}}{3} \ldots \ldots \left( 2 \right)$
Where the formula for buoyancy force is,
$B' = \rho lV'g'$
Here the g’ will be,
$g' = g + \dfrac{g}{3}$
Putting this value in above formula we will get,
$B' = \rho lV'\left( {g + \dfrac{g}{3}} \right)$
Now putting this buoyancy formula in equation $\left( 2 \right)$ we will get,
$\rho lV'\left( {g + \dfrac{g}{3}} \right) = mg + \dfrac{{mg}}{3}$

Taking m common we will get,
$\rho lV'\left( {g + \dfrac{g}{3}} \right) = m\left( {g + \dfrac{g}{3}} \right)$
The mass of the block can also be written as produce of density od the block and its volume
$\rho lV'\left( {g + \dfrac{g}{3}} \right) = \rho bV\left( {g + \dfrac{g}{3}} \right)$
Cancelling the common term we will get,
$\rho lV' = \rho bV$
Putting equation $\left( 1 \right)$ in the above equation we will get,
$\rho lV' = \dfrac{{\rho l}}{2}V$
Cancelling the common terms we will get,
$V' = \dfrac{V}{2}$
Rearranging the above equation we will get,
$\dfrac{{V'}}{V} = \dfrac{1}{2}$
Hence The fraction of volume immersed in liquid will be $\dfrac{1}{2}$.

Therefore the correct option is $\left( A \right)$.

Note: Whenever the whole system will accelerate an external force is applied to balance it. And here the buoyancy force changes because external acceleration is applied on the system and this acceleration is added to the bouncy force. If the whole system will not accelerate and the acceleration only occurs in the block itself then the boynounsy force will not change as the liquid is stable in its place.