Question
Question: A cube of side \(a\) is subjected to shear stress P as shown in the figure. Determine tangential and...
A cube of side a is subjected to shear stress P as shown in the figure. Determine tangential and normal stress along diagonal AC.
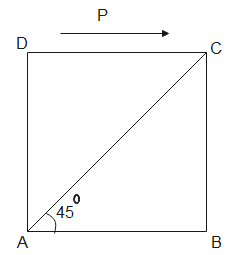
Solution
Stress acting on a body is the force applied per unit area. It causes the shape, area or volume of a body. A shearing force is being applied on the cube; this means that it will change the shape of the cube along its diagonal. The shearing stress is parallel to the area.
Formulas used:
τ=AF
Complete answer:
When a force is applied on a body such that the body gets deformed by slipping between planes, such a force applied per unit area is called the shearing or tangential stress. Its SI unit is Nm−2. It is given by-
τ=AF - (1)
Here, τ is the shearing stress
F is the force applied parallel to its side
A is the displaced area
When a tangential stress, P is applied on cube of side a, it changes its shape as sown in the figure below
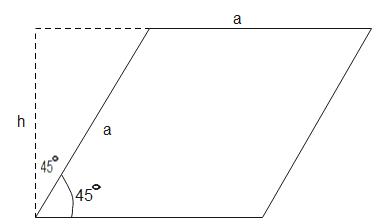
From the above figure,
h=acos45o⇒h=2a
The area of the deformed figure will be-
A=b×h⇒A=a×2a∴A=2a2
The area of the figure is 2a2 sq units.
From eq (1), the shearing stress acting on the cube will be-
τ=2a2P⇒τ=a22P
Therefore, the shearing or tangential stress acting on the cube is a22P.
As there is no tension or compression acting on the cube, the normal stress acting on it is zero.
Therefore, the tangential stress on the cube is a22P and the normal stress is zero.
Note:
Normal stress occurs when a body is kept under compression or tension due to which its dimensions change. The force applied in a shearing stress is parallel to the cross sectional area. After stress is applied, a restoring force is developed in the body which tends to bring it back to its original shape.
