Question
Question: A cube of side \[2\,m\] is placed in front of a concave mirror of focal length \[1\,m\] with its fac...
A cube of side 2m is placed in front of a concave mirror of focal length 1m with its face P at a distance of 3m and face B at a distance of 5m form the mirror. The distance between the images of faces A and B and heights of images of A and B are,respectively
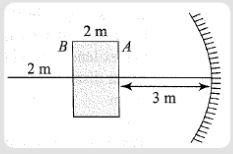
A. 1 m,0.5 m,0.25 m
B. 0.5 m,1m,0.25 m
C. 0.5m,0.25m,1m
D. 0.25m,1m,0.5m
Solution
First using the mirror equation to find the distance between the two points vA and vB then use the magnification relation to find the height of the images for point A and point B.
The formula for the mirror equation is
f1=u1+fv
Here we have to also use the magnification relation. Lens magnification is known as the ratio of an image’s height to an object’s height.
The formula for magnification is ObjectheightImageheight = -ObjectdistanceImagedistance
Complete step by step answer:
Here,
By using the mirror equation,
f1=u1+fv
Here,
For point A,
vA1=−1+31=−32
So,
vA=−23=−1.5
Again,
For point B,
vB1=−1+51=−54
So,
vB=−45=−1.25
Therefore,
The distance between two points is =1.5−1.25=0.25m
Now,
Using the magnification relation, we know that,
