Solveeit Logo
Login

Question

Question: A cube of iron of edge \(5 cm\) floats on the surface of mercury, contained in a tank. Water is then...

A cube of iron of edge 5cm5 cm floats on the surface of mercury, contained in a tank. Water is then poured on top so that the cube just gets immersed. The depth of the water layer in cm is (20+x)(20 + x). (Specific gravities of iron and mercury are 7.8 and 13.6, respectively.) Find the value of xx.

Explanation

Solution

The given question is based on the concept of Archimedes principle. So, using the same will equate the liquid (the mixture of mercury and water) displaced by the cube of iron to the weight of the cube of iron. Thus, finally, the value of the required parameter can be obtained.

Complete answer:
The diagram representing the cube of iron of edge 5cm5 cm floating on the surface of mercury, contained in a tank and the water on top so that the cube just gets immersed is given as follows.

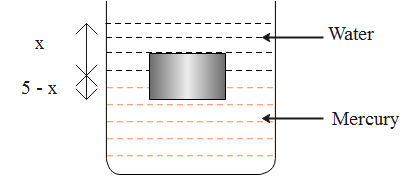
Archimedes principle states that the upward buoyant force exerted by the body fully or partially immersed in a fluid is equal to the weight of the fluid displaced by the body.

Using Archimedes principle,

ρiron×Airon×g=ρmercury×Amercury×g+ρwater×Awater×g{{\rho }_{iron}}\times {{A}_{iron}}\times g={{\rho }_{mercury}}\times {{A}_{mercury}}\times g+{{\rho }_{water}}\times {{A}_{water}}\times g

Substitute the given values in the above equation.

7.8×(5×5×5)×g=13.6×[5×5×(5−x)]×g+1×(5×5×x)×g7.8\times (5\times 5\times 5)\times g=13.6\times [5\times 5\times (5-x)]\times g+1\times (5\times 5\times x)\times g

Continue the further calculation to find the value of xx. Here the value of xx represents the level of water in the tank containing the mixture of mercury and water, that is, the depth of the water level.

7.8×53=13.6×53−13.6×25x+25x7.8\times {{5}^{3}}=13.6\times {{5}^{3}}-13.6\times 25x+25x

Now express the equation in terms of xx.

& 13.6\times 25x+25x=13.6\times {{5}^{3}}-7.8\times {{5}^{3}} \\\ & 340x+25x=1700-975 \\\ & \Rightarrow 365x=725 \\\ \end{aligned}$$ Therefore, the value of $x$ is given as follows. $$\begin{aligned} & x=\dfrac{725}{365} \\\ & x=1.98 \\\ & \Rightarrow x\approx 2 \\\ \end{aligned}$$ **$$\therefore $$ The value of $x$ is $2 cm$, that is, the depth of the water level is $2 cm$ in a tank containing the mixture of mercury and water.** **Note:** As in the question statement, the values of the parameters are given in terms of cm, so, the final answer is provided in cm itself. If they ask to represent the final answer in terms of the SI unit, then we need to convert the unit from cm to meter.