Question

A cube of ice floats partly in water and partly in k.oil. Find the ratio of the volume of ice immersed in water to that in k.oil is (specific gravity of K.oil is 0.8 and that of ice is 0.9).

Answer 1

Firstly, we will find out the density of water and k.oil using their specific gravity values. Then, using the property of buoyancy, we will equate the total weight of the ice with the total force of buoyancy. Using this equated equation, we can find the ratio of the volume of ice immersed in water to that in k.oil.

Complete step by step answer:
The diagram representing the given condition.

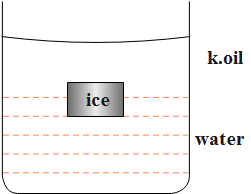
From the question, we have the data as follows.
The specific gravity of kerosene oil = 0.8
The density of the kerosene oil,

& \rho =0.8\times 1000 \\\ & \Rightarrow \rho =800\,\dfrac{kg}{{{m}^{3}}} \\\ \end{aligned}$$ The specific gravity of ice = 0.9 The density of the ice, $$\begin{aligned} & \rho =0.9\times 1000 \\\ & \Rightarrow \rho =900\,\dfrac{kg}{{{m}^{3}}} \\\ \end{aligned}$$ Let the volume of the ice in water be $$=x\,{{m}^{3}}$$ Let the volume of the ice in the kerosene oil be $$=y\,{{m}^{3}}$$ Therefore, the weight of the ice is $$=(x+y)\times 900\,kg$$…… (1) According to buoyancy property, the force applied by the water and the kerosene equals the weight of the ice. So we have the equation, The total force of buoyancy $$=x\times 1000\,kg+y\times 800\,kg$$…… (2) Equate the equations (1) and (2) to find the volume of the ice immersed in water and the volume of the ice immersed in kerosene oil. So, we have, $$\begin{aligned} & (x+y)\times 900=x\times 1000+y\times 800 \\\ & \Rightarrow 900x+900y=1000x+800y \\\ \end{aligned}$$ Continue further calculation $$\begin{aligned} & 1000x-900x=900y-800y \\\ & \therefore 100x=100y \\\ \end{aligned}$$ Therefore, we have, $$x=y$$ The above equation represents that, the volume of the ice immersed in water is equal to the volume of the ice immersed in kerosene oil. As, the volume of the ice immersed in water equals the volume of the ice immersed in kerosene oil, so, the ratio of the volume of ice immersed in water to that in kerosene oil is 1:1. **Note:** As mentioned above, this question is based on the concept of buoyancy. So, using this property definition, that is, in this case, “The force applied by the water and the kerosene equals the weight of the ice”, we have solved this problem. And this is the main step of the calculation. The units of the parameters should be taken care of.