Question

A cube of 4 cm contains a sphere touching its sides. Find the volume $\left( c{{m}^{3}} \right)$ of the gap in between. (Round your answer to the nearest whole number).

Answer 1

Here, in this problem, first we need to draw the figure for only one face of the cube because to show the sphere touching the sides of the cube. To find the volume of the gab we need to subtract Volume of the sphere from the Volume of Cube. Then we will get the answer.

Complete step by step answer:
In this problem, we have to find the volume of the gap for that it is given that the side is 4 cm. For more understanding the given problem, figure is given below:

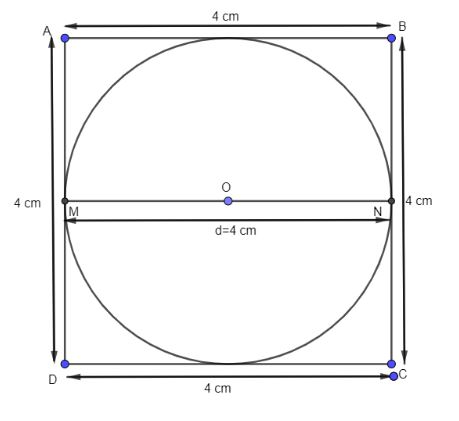
In the above figure, we have drawn the one face of the cube which is ABCD and the sphere touching the all sides of the cube ; hence, instead of considering all the six faces we have considered one face for the purpose of analysis and to get the volume of the gap between the spheres.

Let ABCD be a cube which contains a sphere touching its sides. The diameter of the sphere is the sides of the cube.So, according to the question we need to find the volume of the gap between the volume of the sphere and the cube . To find the volume of the gap we need to subtract the volume of the sphere from the volume of the cube. For that first we have to find the volume of the cube. The volume of cube is given by
$\Rightarrow \text{Volume of cube}=\,side\,\times \,side\times side=\,{{\left( side \right)}^{3}}$
Here, in this question it is given that side is 4 cm after substituting the value in above formula we get:
$\Rightarrow \text{Volume of cube}=\,4\,\times \,4\times 4=\,64\,c{{m}^{3}}---(1)$
Hence, the volume of cube is $64\,c{{m}^{3}}$

Now, we need to find the volume of sphere
Volume of sphere is given by
$\Rightarrow \text{Volume of sphere}=\,\dfrac{4}{3}\pi {{r}^{3}}$
But, according to the question it is given that the side is 4 cm. That means in the case of the sphere, we have the diameter of the sphere as the sides of the cube. That means $d=4\,cm$ by using the relation between diameter and radius is given by $r=\dfrac{d}{2}$
By substituting the value of d, we get:
$\Rightarrow r=\dfrac{4\,cm}{2}=2\,cm$
Substituting the value of r and also, we know the value of $\pi$ is $\dfrac{22}{7}$ in this formula for volume of sphere we get:
$\Rightarrow \text{Volume of sphere}=\,\dfrac{4}{3}\times \dfrac{22}{7}\times {{\left( 2 \right)}^{3}}$

By simplifying this we get:
$\Rightarrow \text{Volume of sphere}=\,\dfrac{4}{3}\times \dfrac{22}{7}\times 8$
By further solving this we get:
$\Rightarrow \text{Volume of sphere}=\dfrac{704}{21}\,c{{m}^{3}}---(2)$
Now, the volume of the gap in between cube and sphere is given by
$\text{Volume}\,\text{of}\,\text{gap}\,\text{between}\,\text{cube}\,\text{and}\,\text{sphere}=\text{Volume}\,\text{of}\,\text{cube}-\text{Volume}\,\text{of}\,\text{sphere}---(3)$
Substituting the value of equation (1) and (2) on equation (3) we get:
$\Rightarrow \text{Volume of gap between cube and sphere}=64-\dfrac{704}{21}$
By taking LCM and cross multiplying we get:

\Rightarrow \text{Volume of gap between cube and sphere}=\dfrac{640}{21} \\\ \therefore \text{Volume of gap between cube and sphere} =30$$ **Therefore, the volume of the gap between the cube and the sphere is $$30\,c{{m}^{3}}$$.** **Note:** One common mistake in such questions is that students forget to write the units, or write the units which are the same as the length. Instead, when we multiply the length three times, the units will also have a cube sign as shown in the answer. Similarly, when finding the area, the units become $$c{{m}^{2}}$$.