Question

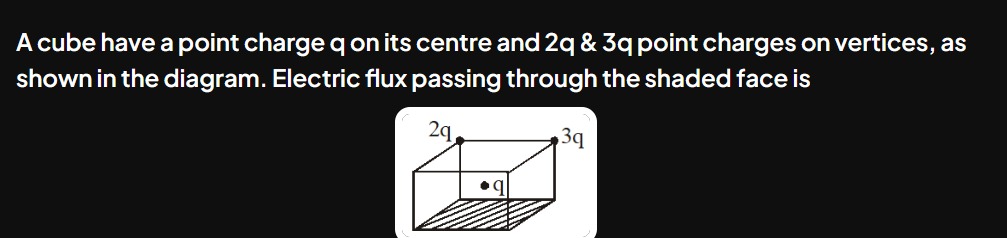
A cube have a point charge q on its centre and 2q & 3q point charges on vertices, as shown in the diagram. Electric flux passing through the shaded face is

Answer 1

3q / (8ε₀)

Answer 2

The problem asks for the electric flux passing through the shaded face of a cube. We need to consider the contribution of each point charge to the flux through this specific face.

1. Flux due to the charge q at the center of the cube: According to Gauss's Law, the total electric flux through a closed surface enclosing a charge Q_enclosed is Φ = Q_enclosed / ε₀. For the charge q at the center, the total flux through the entire cube is Φ_total_q = q / ε₀. Since the charge q is at the exact center, it is symmetrically placed with respect to all six faces of the cube. Therefore, the electric flux passes equally through each of the six faces. The flux through the shaded face (one of the six faces) due to the charge q at the center is: Φ_shaded_q = (1/6) * (q / ε₀)

2. Flux due to charges 2q and 3q at the vertices: For a point charge located at a vertex of a cube, it is shared by 8 identical cubes that meet at that vertex. Thus, only 1/8 of the electric field lines emanating from the charge pass through the volume of the given cube. So, the total flux contributed by a charge Q at a vertex through the entire cube is (1/8) * (Q / ε₀).

A key simplification used in such problems is that the electric flux through any face that contains the vertex where the charge is located is zero. This is because, at the surface, the electric field lines are tangential to the surface, making the dot product E ⋅ dA zero. Each vertex is part of three faces (e.g., for a vertex at (0,0,0), the faces x=0, y=0, z=0 contain it). The remaining three faces do not contain the vertex (e.g., x=L, y=L, z=L for a cube of side L). These three faces are symmetrically equivalent with respect to the vertex charge. Therefore, the total flux passing through the cube from the vertex charge is distributed equally among these three non-adjacent faces. So, the flux through one non-adjacent face due to a charge Q at a vertex is (1/3) * (1/8) * (Q / ε₀) = Q / (24ε₀).

Let's identify the shaded face and the positions of 2q and 3q. The diagram shows the shaded face as the bottom face of the cube. The charge 2q is at a top vertex (e.g., top-front-left). The charge 3q is at another top vertex (e.g., top-front-right). Neither of these top vertices lies on the bottom (shaded) face. Therefore, the shaded face is a "non-adjacent" face for both 2q and 3q.

• Flux due to 2q at a vertex: The shaded face is one of the three faces that do not contain the vertex where 2q is located. Φ_shaded_2q = (2q) / (24ε₀) = q / (12ε₀)

• Flux due to 3q at a vertex: Similarly, the shaded face is one of the three faces that do not contain the vertex where 3q is located. Φ_shaded_3q = (3q) / (24ε₀) = q / (8ε₀)

3. Total Electric Flux through the shaded face: The total flux through the shaded face is the sum of the contributions from all charges: Φ_shaded_total = Φ_shaded_q + Φ_shaded_2q + Φ_shaded_3q Φ_shaded_total = (q / (6ε₀)) + (q / (12ε₀)) + (q / (8ε₀))

To sum these fractions, find the least common multiple (LCM) of the denominators (6, 12, 8), which is 24. Φ_shaded_total = (4q / (24ε₀)) + (2q / (24ε₀)) + (3q / (24ε₀)) Φ_shaded_total = (4q + 2q + 3q) / (24ε₀) Φ_shaded_total = 9q / (24ε₀) Simplify the fraction: Φ_shaded_total = 3q / (8ε₀)

The final answer is $\boxed{\frac{3q}{8\epsilon_0}}$.

Explanation of the solution:

1. Charge at center (q): Flux q/ε₀ is distributed equally among 6 faces. So, flux through one face is q/(6ε₀).
2. Charges at vertices (2q, 3q): For a charge Q at a vertex, the total flux through the cube is Q/(8ε₀). The flux through the 3 faces containing the vertex is zero. The remaining flux Q/(8ε₀) passes equally through the 3 non-adjacent faces. So, flux through one non-adjacent face is Q/(24ε₀).
3. The shaded face is non-adjacent to both 2q and 3q.
4. Total flux through shaded face = q/(6ε₀) (from center charge) + 2q/(24ε₀) (from 2q) + 3q/(24ε₀) (from 3q).
5. Summing these: q/(6ε₀) + q/(12ε₀) + q/(8ε₀) = (4q + 2q + 3q)/(24ε₀) = 9q/(24ε₀) = 3q/(8ε₀).