Question

A crown glass prism and a flint glass prism are combined to produce dispersion without deviation. Mean refractive indices of crown and flint glass are respectively 1.5 and 1.6. Ratio of angle of crown glass prism to that of flint prism is
(A). 1.06
(B). 0.9375
(C). 1.2
(D). 1.5

Answer 1

In order to find the ratio we will use the formula of dispersion for no deviation, then we will proceed further by putting the values of mean refractive indices as given in the problem statement to find the solution.

Formula Used:
${\theta _f}({i_f} - 1) = {\theta _c}({i_c} - 1)$

Complete step-by-step answer :

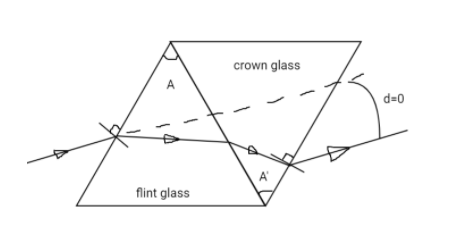
Given that
The refractive index of flint glass is ${i_f} = 1.62$
The refractive index of crown glass is ${i_c} = 1.518$
We know that
Dispersion for no deviation is given as
${\theta _f}({i_f} - 1) = {\theta _c}({i_c} - 1)$
Where ${\theta _c}$ = angle of crown glass prism
And ${\theta _f}$ = angle of flint glass prism
So, let us find ratio of angle of crown glass prism to that of flint prism by manipulating the values in the equation:
$\because {\theta _f}({i_f} - 1) = {\theta _c}({i_c} - 1) \\\ \Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} = \dfrac{{({i_f} - 1)}}{{({i_c} - 1)}} \\\$
Now, let us substitute the values in order to find the ratio:
$\Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} = \dfrac{{({i_f} - 1)}}{{({i_c} - 1)}} \\\ \Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} = \dfrac{{(1.62 - 1)}}{{(1.518 - 1)}} \\\ \Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} = \dfrac{{0.62}}{{0.518}} \\\ \Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} = 1.1969 \\\ \Rightarrow \dfrac{{{\theta _c}}}{{{\theta _f}}} \simeq 1.2 \\\$
Hence the ratio of angle of crown glass prism to that of flint prism is 1.2
So, the correct answer is option C.

Note : The term that is used in the optics to represent the ratio of the light speed in vacuum and light speed in a medium is known as the refractive index. By using the refractive index, the bending of ray (light ray) can be obtained. Refractive index of a medium is constant. In order to solve such problems, students must remember the formula for dispersion of light.