Question

A cricket ball is hit at an angle of $30^\circ$ to the horizontal with kinetic energy E. What is its kinetic energy, when it reaches the highest point?
A. $\dfrac{{\text{E}}}{2}$
B. $0$
C. $\dfrac{{2{\text{E}}}}{3}$
D. $\dfrac{{3{\text{E}}}}{4}$

Answer 1

Hint: When the ball reaches the highest point, its vertical component of velocity becomes zero, but the horizontal component remains the same as it was initially. So, K.E can be solved by formula $\dfrac{1}{2}{\text{m}}{{\text{v}}^2}$

Step by step answer:
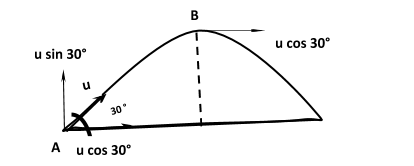
Let's say the ball is hit at point A at an angle of $30^\circ$ with horizontal. Suppose its initial velocity is u. So the horizontal is ${\text{u}}\cos 30^\circ$ and the vertical component is ${\text{u}}\sin 30^\circ$.

${\text{E}} = \dfrac{1}{2}{\text{m}}{{\text{u}}^2}$…………. equation (1)
When the ball reaches the height point (i.e. at B), its vertical component will become zero because it is already at its highest point and cannot go further up. But under the influence of gravity (which acts downward), there will be no change in its horizontal velocity.
So, at the highest velocity is ${\text{u}}\cos 30^\circ$. Therefore, kinetic energy at B is:
${\text{K}}{\text{.}}{{\text{E}}_{\text{B}}} = \dfrac{1}{2}{\text{mv}}_{\text{B}}^2$
$= \dfrac{1}{2}{\text{m}}{\left( {{\text{u cos 30}}^\circ } \right)^2}$
$= \dfrac{1}{2}{\text{m}}{\left( {{\text{u}} \times \dfrac{{\sqrt 3 }}{2}} \right)^2}$
${\text{K}}{\text{.}}{{\text{E}}_{\text{B}}} = \dfrac{3}{8}{\text{m}}{{\text{u}}^2}$………….. equation (2)
So, now divide equation (2) by equation (1)
$\dfrac{{{\text{K}}{\text{.}}{{\text{E}}_{\text{B}}}}}{{\text{E}}} = \dfrac{{\dfrac{3}{8}{\text{m}}{{\text{u}}^2}}}{{\dfrac{1}{2}{\text{m}}{{\text{u}}^2}}}$
${\text{K}}{\text{.}}{{\text{E}}_{\text{B}}} = \dfrac{3}{4}{\text{E}}$
So, the answer is (D).

Note: The vertical component of velocity is zero at highest point but that does not mean acceleration is also zero. At highest point acceleration is g (i.e. acceleration due to gravity having value $9.81\dfrac{{\text{m}}}{{{{\text{s}}^2}}}$).