Question
Question: A crate of mass m is being pulled (by an engine) up on an inclined plane making an angle \(\alpha\) ...
A crate of mass m is being pulled (by an engine) up on an inclined plane making an angle α with the horizontal. The coefficient of friction between crate and incline is μ. The crate starts from rest and is pulled by the engine at constant acceleration such that it travels a distance (displacement) s in time t. Determine the power delivered by engine to crate as a function of time. Take t=0 as the instant when crate is at rest.
A. mg(sinα+μcosα)×t2s
B. μmgcosα×t2s
C. t34ms2
D. 42ms[t22s+g(sinα+μcosα)]
Solution
The best way to go about this problem is to sketch out a free body diagram and determine all the influencing forces and their directions. Account for the pulling force of the engine, gravitational force of the create, normal reaction on the crate, frictional force on the crate, force due to acceleration of the crate, and all of their component directions with respect to the angle of inclination.
Then, from the FBD equations determine the net pulling force acting on the crate. This, with the distance travelled by the create, gives the work done by the engine in pulling the crate, and this work down as a rate of change gives the power delivered by the engine to the crate, which is what we need.
Formula Used:
Frictional force: Fr=μN
Work done: W=F.s
Power: P=dtdW
Complete step by step answer:
We know that the frictional force acting on the crate is given by: Fr=μN, where μ is the coefficient of friction and N is the normal reaction force acting on the crate.
From the FBD we see that the normal reaction of the inclined plane is in response to the cosine component of the gravitational force acting downwards, i.e., N=mgcosα
⇒Fr=μmgcosα
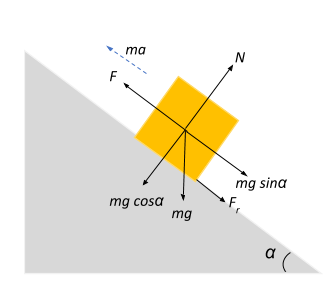
Now, let us look at the influencing forces parallel to the inclined plane:
F−Fr−mgsinα=ma⇒F=Fr+mgsinα+ma⇒F=μmgcosα+mgsinα+ma
The work done by the engine in pulling the crate up the incline can be given as a function of distance as:
W=F.s=(μmgcosα+mgsinα+ma).s
Now, using the kinematic equation of motion: s=ut+21at2, we have the initial velocity of the crate u=0, acceleration of the crate a, travelling a distance s in time t. Therefore, the equation becomes:
s=21at2
Substituting this in our work equation, we get:
W=(μmgcosα+mgsinα+ma).(2at2)
Now, we know that power can be defined as the energy expenditure or the rate of change of work done over time t:
⇒P=dtdW
⇒P=dtd(μmgcosα+mgsinα+ma).(2at2)=(μmgcosα+mgsinα+ma).(at)
From s=21at2 we have a=t22s
⇒P=(μmgcosα+mgsinα+m(t22s)).(t22s)t=(μmgcosα+mgsinα+m(t22s)).(t2s)
⇒P=m[g(μcosα+sinα)+t22s]t2s=[g(μcosα+sinα)+t22s]t2ms
Therefore, the power delivered by the engine to the crate in pulling it up the incline is given by the option D. 42ms[t22s+g(sinα+μcosα)]
Note:
It is very important to remember to separate the components of forces and choose the correctly contributing component for each direction. Also, do not forget to include the coefficient of friction while determining the frictional force.
It is also crucial to remember the sign convention for work done. If any force retards the motion of a body, the work done by that force will be negative but if a force contributes to the motion of the body the work done by that force will be positive.
We take the power to be the rate of change of work, which is nothing but the work done over a time t because this is analogous to the more familiar definition of power that we know, which is energy transfer per unit time from the engine and the crate, which is what happens when the engine pulls the crate up the incline anyways.
