Question

A cork is submerged in water by a spring attached to the bottom of a bowl. When the bowl is kept in an elevator moving with acceleration downwards, the length of spring:

Answer 1

In order to answer the above question, we will understand a basic term of fluid mechanics, i.e., the phenomenon of buoyancy. We will draw the free body diagram of the following situation and will evaluate the forces acting on the cork. Using this, we will conclude our answer to what will happen to the length of the spring if the system is placed in an elevator and is accelerating downwards.

Complete step by step answer:
First of all, we will discuss a term known as the buoyant force. The force that allows objects to float is known as buoyancy. It's the force applied to an object that's partially or completely submerged in a liquid. The difference in pressure acting on opposite sides of an object immersed in a static fluid causes buoyancy. The buoyant force is another name for it. The phenomenon of buoyancy is caused by the Buoyant Force.

The buoyant force is the upward force exerted on an object that is fully or partially submerged in a fluid, as previously stated. Up-thrust is another name for this upward force.A body immersed partly or completely in a fluid tends to lose weight, i.e. appears to be lighter, due to the buoyant force.The equation of the buoyant force is written as:
${{F}_{b}}=\rho Vg$
Where $\rho$ is the density of the liquid, $V$ is the volume of the object immersed into the liquid and $g$ is the gravitational acceleration.

Now, we will draw a diagram using the data given in the question.

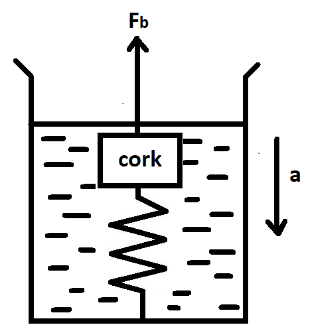
As we can see in the figure, a cork having mass $m$ is fully submerged into the water in a bowl with the help of the spring having a spring constant $k$. As the cork has a density that is lower than that of the water, the cork tries to pull itself upwards from the water and this upward force ${{F}_{b}}$ is due to the phenomenon of buoyancy. The whole system is then kept in an elevator and is moving downwards with an acceleration of $a$.

Now, if we draw a free body diagram of the above system before keeping it into the elevator, the forces acting on the cork are as follows:

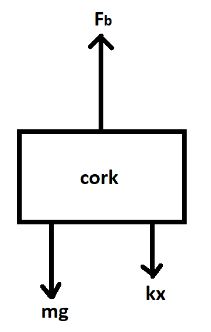
There Is a downward force acting on the cork due to the gravitational acceleration and is given by ${{F}_{g}}=mg$. There is a restoring force which is acting in the downward direction due to the spring. This force is given with the help of Hooke’s Law as ${{F}_{s}}=kx$. Lastly, there is an upward force due to the phenomenon of buoyancy. This force is given by ${{F}_{b}}=\rho Vg$. As the system is in equilibrium before it is kept in an elevator, the equation of forces can be written as,
{{F}_{g}}+{{F}_{s}}={{F}_{b}} \\\ \Rightarrow mg+kx=\rho Vg \\\
Now, when the system is placed in an elevator and is going down with an acceleration $a$, the buoyant force is changed due to this and is given by
${{F}_{b}}'=\rho V(g-a)$
Therefore, the system will no more be in an equilibrium state as
$m(g-a)+kx\ne \rho V(g-a)$
From this, we can conclude that if the buoyant force decreases, i.e., the force acting in the upward direction decreases.

Hence, the downward force acting on the cork becomes dominant. Therefore, the length of the spring will be decreased.

Note: It is important to note that the above problem is solely dependent on the densities of the liquid as well as the material which is submerged inside the liquid. In the case discussed above, the cork has a density which is lower than that of the water and hence, the length of the spring is decreased when the buoyant force is decreased. Whereas, if the density of the material which is submerged is having a density which is greater than that of the water, the spring will be compressed in the initial condition and its length will increase with the decrease in the buoyant force.