Question

A cord is wound around the circumference of a wheel of radius ‘r’. The axis of the wheel is horizontal and the moment of inertia about it is ‘I’. The weight ‘mg’ is attached to the end of the cord and falls from rest. After falling through a distance ‘h’, the angular velocity of the wheel will be
A. ${\left[ {{\text{mgh}}} \right]^{1/2}}$
B. ${\left[ {\dfrac{{2{\text{mgh}}}}{{{\text{I}} + 2{\text{m}}{{\text{r}}^{\text{2}}}}}} \right]^{1/2}}$
C. ${\left[ {\dfrac{{2{\text{mgh}}}}{{{\text{I}} + {\text{m}}{{\text{r}}^{\text{2}}}}}} \right]^{1/2}}$
D. ${\left[ {\dfrac{{{\text{mgh}}}}{{{\text{I}} + {\text{m}}{{\text{r}}^{\text{2}}}}}} \right]^{1/2}}$

Answer 1

Use the law of conservation of energy to solve this question. The initial total energy of the system of wheel and weight is due to gravitational potential energy of the weight. The final total energy involves rotational kinetic energy of the wheel as well as kinetic energy of the weight.

Formula used:

1. Gravitational potential energy, $U = mgh$, where, m is the mass, g is the acceleration due to gravity and h is the height above the ground.
2. Kinetic energy, $K = \dfrac{1}{2}m{v^2}$, where v is the velocity of the body.
3. Rotational kinetic energy, $K = \dfrac{1}{2}I{\omega ^2}$, where, I is the moment of inertia and $\omega$ is the angular velocity.

Complete step by step answer:
We have given that initially the system of wheel and weight is at rest. After the weight falls from the rest, the wheel attains an angular velocity that’s what we want to determine.

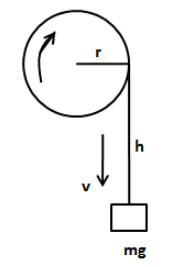
We can apply the law of conservation of energy to determine the angular velocity of the wheel as follows,
${U_i} + {K_i} = {U_f} + {K_f}$
Here, U is the potential energy and K is the kinetic energy. The subscripts “i” and “f” denotes initial and final value respectively.

The initial total energy will be the potential energy of the weight at height h. After the weight falls to a distance h, the final energy will be the sum of potential energy of the weight which is zero, kinetic energy of the weight and rotational kinetic energy of the wheel.
Therefore, we can write the above equation as,
$mgh = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2}$
Here, v is the velocity of the weight, I is the moment of inertia of the wheel and $\omega$ is the angular velocity of the wheel.

We know the relation, $v = r\omega$. Therefore, after substituting $v = r\omega$ in the above equation, we get,
$mgh = \dfrac{1}{2}m{\left( {r\omega } \right)^2} + \dfrac{1}{2}I{\omega ^2}$
$\Rightarrow mgh = \dfrac{1}{2}m{r^2}{\omega ^2} + \dfrac{1}{2}I{\omega ^2}$
$\Rightarrow mgh = \dfrac{1}{2}\left( {I + m{r^2}} \right){\omega ^2}$
$\therefore \omega = {\left[ {\dfrac{{2{\text{mgh}}}}{{{\text{I}} + {\text{m}}{{\text{r}}^{\text{2}}}}}} \right]^{1/2}}$

So, the correct answer is option (C).

Note: To solve such types of questions, students should always draw a rough diagram of the given situation. The potential energy always decreases when the body falls from a height. Here, we have taken the gravitational potential energy at the final position as zero assuming it is close to ground.