Question

A copper rod of length l is rotated about one end, perpendicular to the uniform magnetic field B with constant angular velocity $\omega$. The induced emf between two ends of the rod is:
A. $\dfrac{1}{2} B \omega l^2$
B. $B \omega l^2$
C. $\dfrac{3}{2} B \omega l^2$
D. $2 B \omega l^2$

Answer 1

This question is from the topic motional emf. By Faraday's law when the rod will be rotated in a magnetic field, emf will be induced across its ends due to change in magnetic flux. Consider the rod to be simply a length and perform integration by considering dx of that length.
Formula used:
The emf induced due to change in magnetic flux associated with moving length l, is given as:
$e = - \dfrac{d \phi}{dt} = Blv$.

Complete answer:
We know that the magnetic flux through an area is given by:
$\phi = BA$.
But we are dealing with a rod of length l which is moving. The flux through the rod is only due to its length and change in flux is due to its velocity. So, for the entire rod, we may write the emf induced as
$e = Blv$.
Now, this rod is rotating in the magnetic field and the flux through it will change inducing an emf. This motion is not similar to linear motion. So, we consider a small length dx of the rod which happens to be performing a circular motion with angular velocity $\omega$.
The rate of change of flux or the emf induced is:
$e_1 = B v dx$.

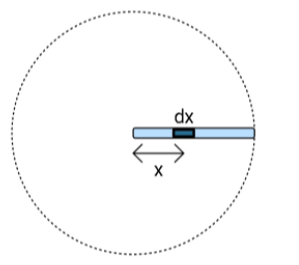
Now, in circular motion we know that the velocity is given as:
$\dfrac{dx}{dt} = v = x \omega$
as, we assumed the distance of dx from the axis to be x.
The emf induced due to dx can be written as:
$e_1 = B \omega x dx$ ;
integrating this from the limits 0 to l will give us the required emf e.
$e = B \omega \int_{0}^{l}xdx = B \omega \left( \dfrac{x^2}{2} \right)_0^l = \dfrac{1}{2} B \omega l^2$.

Therefore, the correct answer is option (A).

Note:
The formula e = Blv is for the case of linear motion. Do not substitute the value of v directly into this to get the required emf as it should be understood that a rod performing circular motion has different velocity v throughout its length. The angular velocity for the entire rod is the same but the linear velocity will be different throughout the length of the rod.