Question

A copper ring is suspended by a thread in a vertical plane. If one end of a magnet is brought horizontally towards the ring in plane of a ring as shown, the ring will

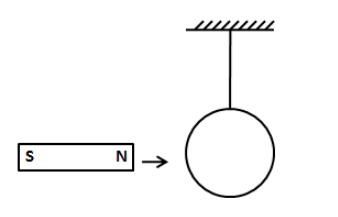
A. Move towards the magnet
B. Not change its position
C. Move away from the magnet
D. Firth move towards and then move away from the magnet

Answer 1

Faraday’s law states that the changing magnetic field induces current in the loop. The magnetic flux is proportional to the cosine of the angle between the magnetic field and area vector of the ring. As long as there is no flux around the ring, the magnetic field will not develop in the ring.

Complete answer:
As we know, from Faraday’s law, the changing magnetic field induces current in the loop. The changing magnetic field is associated with the magnetic flux and the magnetic flux of the circular coil is given as,
$\phi = BA\cos \theta$
Here, B is the magnetic field, A is the area vector and $\theta$ is the angle between the magnetic field and area vector.

In the above figure, the magnet is brought close to the copper ring in the plane of the ring. Therefore, since the area vector of the copper ring is perpendicular to the plane of the ring, the angle $\theta$ will be $90^\circ$.
Substituting $90^\circ$ for $\theta$ in the above equation, we get,
$\phi = BA\cos \left( {90} \right)$
$\therefore \phi = 0$
Therefore, we can see, there will not be induced current in the ring as the change in the flux is zero. The magnetic field induced in the ring will also be zero and the ring will behave as non-magnet. So, the ring will be unaffected by the magnetic field of the magnet.

So, the correct answer is option B.

Note: The area vector is always perpendicular to the plane of the object. Note that the flux associated with the magnetic field will be the maximum when the area vector and the magnetic field have the same direction. For the current to induce in the ring, the magnet should be brought closer to the ring perpendicular to the plane of the ring.