Question
Question: A coolie is pushing a box weighing \(1500N\) up an inclined plane 7.5m long on to a platform, 2.5m a...
A coolie is pushing a box weighing 1500N up an inclined plane 7.5m long on to a platform, 2.5m above the ground.
(i) Calculate the mechanical advantage of the inclined plane.
(ii) Calculate the effort applied by the coolie.
(iii) In actual practice, the coolie needs to apply more effort than what is calculated. Give one reason why you think the coolie needs to apply more effort.
Solution
Mechanical advantage of the inclined plane is the ratio of the length of the inclined plane and its height from the ground. Substitute the values of height and length of the inclined plane to calculate the mechanical advantage. Mechanical advantage is also defined as the ratio of the load and the effort. Substitute the obtained mechanical advantage value and the load to find the value of the effort applied by the coolie.
Complete step by step answer:
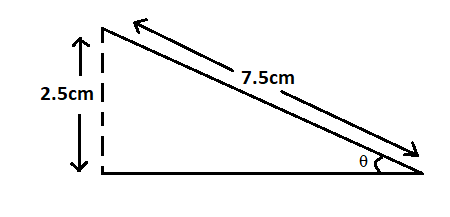
We are given that a coolie is pushing a box weighing 1500N up an inclined plane 7.5m long on to a platform, 2.5m above the ground.
(i) The mechanical advantage of the inclined plane.
Mechanical advantage (MA) is the ratio of the length of the inclined plane to its vertical height from the ground.
MA=heightlength
Length of the inclined plane given is 7.5 cm.
Height of the inclined plane from the ground is 2.5 cm.
MA=hl l=7.5cm,h=2.5cm MA=2.57.5 MA=3
The mechanical advantage of the inclined plane is 3.
(ii) The effort applied by the coolie.
Mechanical advantage can also be defined as the ratio of the weight of the load and the force (effort) applied to pull it up.
MA=effortload
Effort applied is obtained by dividing the Mechanical advantage with the load.
MA=effortload Effort=MAload load=1500N,MA=3 ⟹Effort=31500 ∴Effort=500N
The effort applied by the coolie is 500N.
(iii) In actual practice, the coolie needs to apply more effort than what is calculated. Give one reason why you think the coolie needs to apply more effort.
In actual practice, there will be friction generated between the inclined plane and the bottom of the box which is pulled over the plane. The coolie also has to work against the frictional force generated. So, the effort needed to be applied by the coolie will be more than 500N.
Note:
Here we have calculated the effort only when gravitational force is acting upon the box. But every inclined plane generates friction with the load and therefore, the effort must also be calculated to oppose the frictional force.
