Question

A cook uses the fire tongs of length $28cm$ to lift a piece of burning coal of mass $250g$. If he applies the effort at a distance of $14cm$ from the fulcrum, find the effort in S.I. unit. Take $g = 10m{s^{ - 2}}$.

Answer 1

The length of the fire tongs can be assumed as the length of the load arm and the distance at which the cook applies the effort can be assumed as the length of the effort arm. Since the product of load with load arm and the effort with effort arm is equal, the effort can be calculated.
Formula used:
$L \times {d_L} = E \times {d_E}$

Complete step by step solution:
The fulcrum in case of fire tongs is situated at one of its ends $A$ and the load is lifted at its other end $B$, the effort is applied at a point $C$ between both ends $A$ and $B$. The following diagram makes it clear-

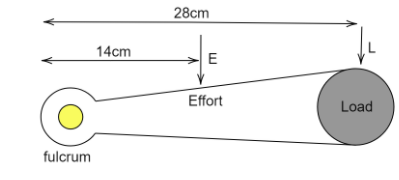
We know that,
$L \times {d_L} = E \times {d_E}$
where$L$ is the weight of the load.
${d_L}$is the length of the load arm.
$E$is the effort applied to lift the load.
${d_E}$is the length of the effort arm.
In the question, it is given that mass of the load, $M = 250g$
Writing the mass of the load in SI units, we have-
$250g = 0.25kg$ $\\{ 1kg = 1000g\\}$
Weight of the load, $W = Mg$
Taking$g = 10m{s^{ - 2}}$,
$W = 0.25 \times 10 = 2.5N$
The length of the load arm, ${d_L} = 28cm$
The length of the effort arm, ${d_E} = 14cm$
Putting these values in the above formula,
$2.5 \times 28 = E \times 14$
Upon rearranging we get,
$E = \dfrac{{2.5 \times 28}}{{14}}$
$\Rightarrow E = 2.5 \times 2 = 5$

Hence, the effort applied by the cook to lift the piece of burning coal is $5N$.

Note: Effort and load, both are a form of force. The SI unit of force is Newton. It is defined as a force that can produce an acceleration equal to $1m/{s^2}$ in a body having a mass of $1kg$. Therefore it is important to convert the mass of the load into kilograms so that its weight can be in Newton.