Question

A convex surface separates two media of refractive indices $1.4$ and $2.1$. If the radius of curvature is $25{\text{ }}cm$ and then the image is obtained in denser medium at a distance of $400{\text{ }}cm$, then calculate the distance between the object and the surface.

Answer 1

We will make use of the given values and use the formula of finding object distance and image distance of the refracting spherical surfaces. As the image is observed in the denser medium then object distance will have negative direction.

Complete step-by-step solution:
The bending of light rays when it falls into the surface of another medium is known as refraction. If the light falls from rarer medium to denser medium then it bends inwards, while if it travels from denser medium to rarer medium it bends outward.

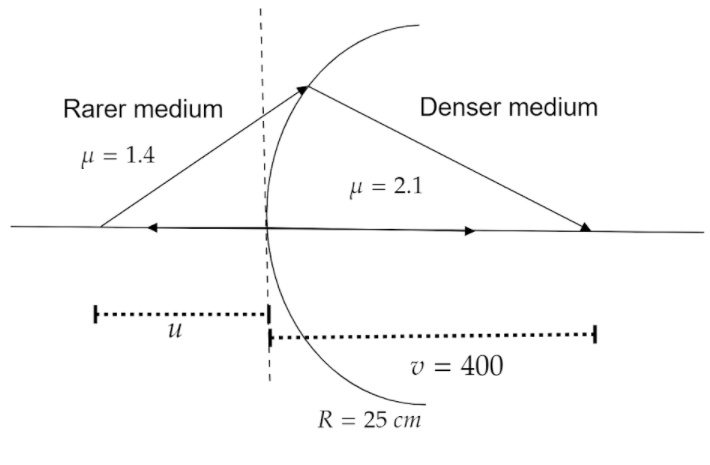
The equation of refraction of light falling in two different medium is,
$\dfrac{{{\mu _2}}}{v} + \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{R} - - - - - \left( 1 \right)$
The variables are defined as-
${\mu _2}$ is defined as the refractive index of a denser medium.
${\mu _1}$ is defined as the refractive index of a rarer medium.
$v =$ image distance.
$u =$object distance.
$R$ is the radius of curvature of the spherical mirror.
According to the given question the values of the given variables are as follows-
${\mu _2} = 2.1$, ${\mu _1} = 1.4$, $v = 400$ and $R = 25$.
The value of $u$ is negative as it is on the left side of the mirror.
Substituting these values in equation $\left( 1 \right)$ we get,
$\dfrac{{2.1}}{{400}} - \dfrac{{1.4}}{u} = \dfrac{{2.1 - 1.4}}{{25}}$
Simplifying the equation we get,
$u = 27.2$
The distance between the object and the surface of the spherical mirror is $27.2{\text{ }}m$.

Note: It must be noted that the right part from the pole of a mirror is considered to be positive while the part left to the pole of the mirror is considered to be negative. The upper part of the principal axis is considered to be positive and the lower part is considered to be negative.