Question

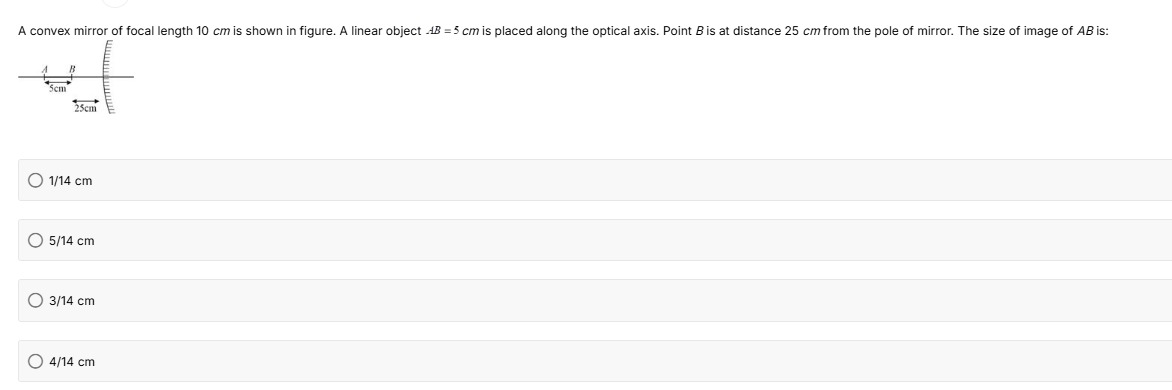
A convex mirror of focal length 10 $cm$ is shown in figure. A linear object $\overline{AB}=5$ $cm$ is placed along the optical axis. Point $B$ is at distance 25 $cm$ from the pole of mirror. The size of image of $\overline{AB}$ is:

• A. 1/14 cm
• B. 5/14 cm
• C. 3/14 cm
• D. 4/14 cm

Answer 1

Answer: (B)

5/14 cm

Answer 2

The problem involves finding the size of the image of a linear object placed along the optical axis of a convex mirror. Given: Focal length of the convex mirror, $f = +10$ cm. Object length, $AB = 5$ cm. Point B is at a distance of 25 cm from the pole. From the figure, point B is closer to the mirror than point A. Object distance for point B, $u_B = -25$ cm. Object distance for point A, $u_A = -(25 + 5) = -30$ cm.

We use the mirror formula: $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$

For point B: $\frac{1}{v_B} = \frac{1}{f} - \frac{1}{u_B} = \frac{1}{10} - \frac{1}{-25} = \frac{1}{10} + \frac{1}{25} = \frac{5+2}{50} = \frac{7}{50}$ $v_B = \frac{50}{7} \text{ cm}$

For point A: $\frac{1}{v_A} = \frac{1}{f} - \frac{1}{u_A} = \frac{1}{10} - \frac{1}{-30} = \frac{1}{10} + \frac{1}{30} = \frac{3+1}{30} = \frac{4}{30} = \frac{2}{15}$ $v_A = \frac{15}{2} \text{ cm}$

The image of the object $\overline{AB}$ is the segment between the images of points A and B. The size of the image is the absolute difference between their image distances. Size of image $= |v_A - v_B|$ $|v_A - v_B| = \left|\frac{15}{2} - \frac{50}{7}\right| = \left|\frac{15 \times 7 - 50 \times 2}{14}\right| = \left|\frac{105 - 100}{14}\right| = \frac{5}{14} \text{ cm}$