Question

A convex lens of focal length $f$ is cut into halves as shown. Light rays parallel to the principal axis are incident on one half of the lens (say ${L_1}$). This will form an image at:

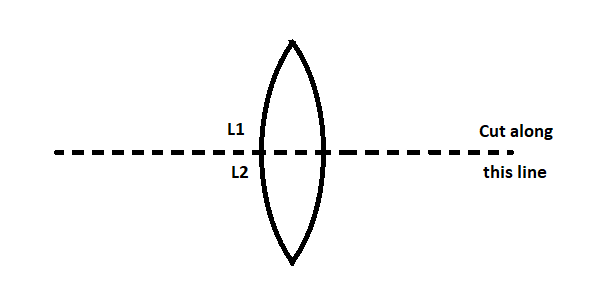
(A) $f$
(B) $\dfrac{f}{2}$
(C) $2f$
(D) $\dfrac{f}{4}$

Answer 1

A convex lens is said to be cut into two halves as shown in the diagram along the principal axis of the lens. The incident light rays are assumed to be parallel to the principal axis. It will be falling on one half of the lens. We assume it to be the upper part ${L_1}$ of the lens. Now we have to find the point where the image is formed.

Complete step by step solution:
We know that the lens is cut horizontally along the principal axis. Therefore there will not be any change in the radius of curvature of the lens. It will remain the same.
According to lens makers formula, the focal length of the lens is given by
$\dfrac{1}{f} = (n - 1)\left[ {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right]$
Where $f$stands for the focal length of the lens, $n$stands for the refractive index of the lens and ${R_1}$and ${R_2}$stands for the radii of curvature of the lens.
Since there will not be any change in the radii of curvature of the lens ${R_1}$and${R_2}$will remain the same before and after cutting the lens into two halves. Therefore there will not be any change in the focal length of the lens. The focal length will remain the same before and after cutting the lens.
The answer is:

Option (A): $f$

Note:
A lens that converges a light beam passing through it is called a converging lens. A convex lens is a converging lens. If a lens diverges the light beam it is called a diverging lens. A concave lens is a diverging lens. The distance between the optic center and the principal focus of the lens is called the focal length of the lens.