Question
Question: A convex lens of focal length ‘f’ cut into parts first horizontally and then vertically. Find the fo...
A convex lens of focal length ‘f’ cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown.
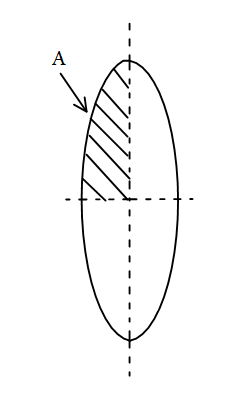
A) 2f
B) f
C) 4f
D) 2f
Solution
The formula for calculating the focal lengths can be used here to find the correct answer for this problem. Also when we cut the lens horizontally the focal length does not change, the focal length of the lens changes when the lens is cut vertically.
Formula used:
The formula of the focal length is given by f1=(μ−1)(R11−R21) where f is the focal length μ is the refractive index R1 is the radius of lens of the left surface of lens and R2 is the radius of the lens of the right surface.
Complete step by step answer:
When the lens is cut horizontally then the focal length of the lens but when the lens is cut vertically then the focal length of the lens changes.
The focal length of the lens is given by,
⇒f1=(μ−1)(R11−R21)Where f is the focal length μ is the refractive index R1 is the radius of lens of the left surface of lens and R2 is the radius of the lens of the right surface.
If both of the surfaces of lens are of equal radius then the focal length of the lens is given by,
⇒f1=(μ−1)(R11−R21)Where R1=R2=R
⇒f1=(μ−1)[R1−(−R1)]
⇒f1=(μ−1)[R1+R1]
⇒f1=(μ−1)[R2]
⇒f=2(μ−1)R………eq. (1)
As the lens is cut vertically the half of the lens is cut away, therefore R2=0.
⇒f21=(μ−1)(R11)
⇒f21=(μ−1)(R1)
⇒f2=(μ−1)R………eq. (2)
Dividing equation (2) by (1).
⇒ff2=2(μ−1)R(μ−1)R
⇒ff2=2
⇒f2=2f
The focus of the part A of the lens is f2=2f. So the correct option for this problem is option D.
Note:
It is advisable to students to remember and understand the lens formula as it helps to solve these types of problems. The sign of the R2 is negative because the centre of the lens is considered as origin and the left side is negative.
