Question

A convex lens of focal length $20cm$ is placed coaxially with a convex mirror of radius of curvature$20cm$ . The two are kept $15cm$ apart. A point object is placed $40cm$ in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation.

Answer 1

Hint:- In this question, we can find the distance of the image ${I_1}$ by using the convex lens formula. After finding the position of ${I_1}$, we can find the position of ${I_2}$ by using a convex mirror formula.

Complete step-by-step solution :

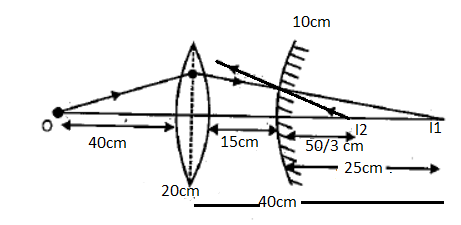
According to the question, a point object is placed at ${u_l} = 40cm$from a convex lens of focal length ${f_l} = 20cm$.
We have the lens formula for convex lens,
$\dfrac{1}{{{v_l}}} - \dfrac{1}{{{u_l}}} = \dfrac{1}{{{f_l}}}$
Putting the values of ${u_l} = 40cm$and ${f_l} = 20cm$, we get-
$\dfrac{1}{{{v_l}}} - \dfrac{1}{{ - 40}} = \dfrac{1}{{20}} \\\ \Rightarrow {v_l} = 40cm \\\$
Now, from the ray diagram, image ${I_1}$( at the distance $v = 40cm$) is formed by the convex lens which becomes an object for the convex mirror.
The distance between lens and mirror is $15cm$ . So, for the convex mirror.
${u_m} = 40 - 15 \\\ {u_m} = 25cm \\\$
Now, if the $R$ is the radii of curvature then the focal length ${f_m}$ of convex mirror,
${f_m} = \dfrac{R}{2} \\\ \Rightarrow {f_m} = 10cm \\\$
We have the mirror equation for the convex mirror,
$\dfrac{1}{{{v_m}}} + \dfrac{1}{{{u_m}}} = \dfrac{1}{{{f_m}}}$
$\dfrac{1}{{{v_m}}} + \dfrac{1}{{25}} = \dfrac{1}{{10}} \\\ \Rightarrow {v_m} = \dfrac{{50}}{3}cm \\\$
Hence, the image ${I_2}$ is formed at $\dfrac{{50}}{3}cm$ at the right side of the convex mirror. The position of final image from the convex lens is given as-
$\dfrac{{50}}{3} + 15 = \dfrac{{95}}{3}cm$
We know that the image formed by the convex mirror is always erect and virtual. So, ${I_2}$ is a virtual image.
Hence, the final image is formed at $\dfrac{{50}}{3}cm$ at the right side of the convex mirror and the final image is virtual as well as erect.

Note:- In this question, we have to note that there are two images formed. The image from the convex lens becomes the object for the convex mirror. The distance of the object (first image)${u_m}$ from the mirror will be found by subtracting $15cm$ from the ${v_l}$. We have to remember that the image formed by a convex mirror is always erect and virtual.