Question
Question: A convex lens in air produces a real image having the same size as object. When the object and the l...
A convex lens in air produces a real image having the same size as object. When the object and the lens are immersed in a liquid, the real image formed is enlarged three times the object size. Find the refractive index of the liquid. (μglass=1.5)
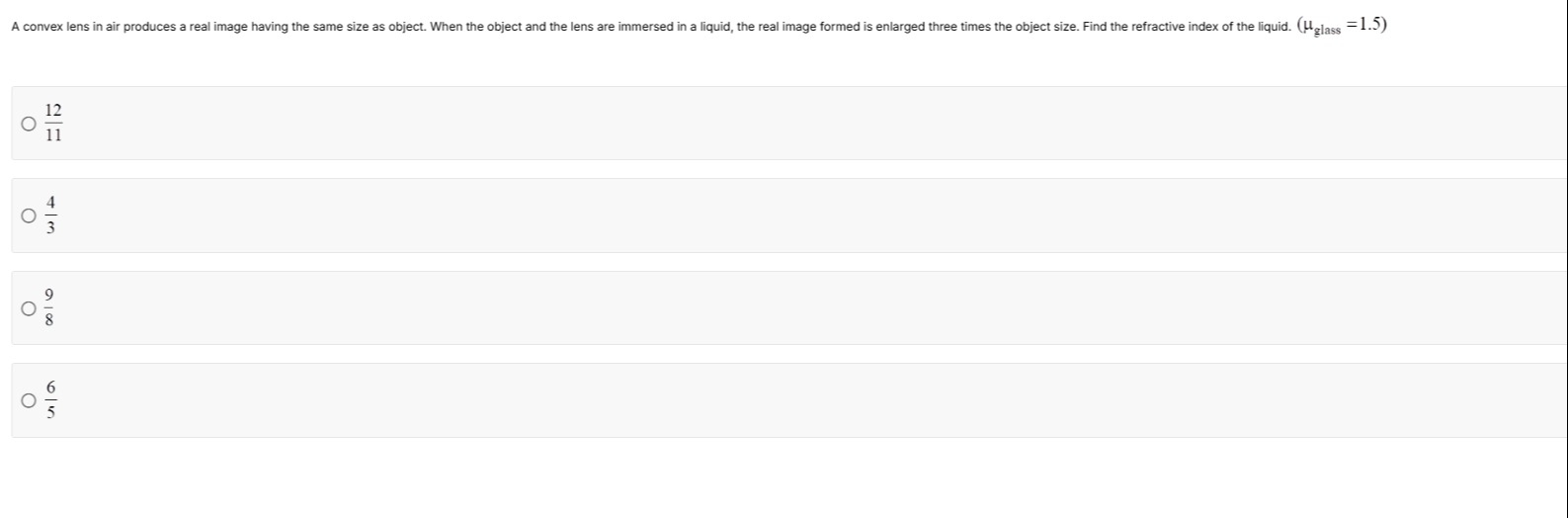
1112
34
89
56
89
Solution
Here's how to solve this problem:
1. Analyze the lens in air:
When a convex lens in air produces a real image of the same size as the object, it implies that the object is placed at twice the focal length (2Fa).
- Magnification M=−1 (real and inverted image).
- Object distance u=−2Fa.
- Image distance v=2Fa.
- The magnitude of the object distance is ∣u∣=2Fa.
The lens maker's formula for a lens in air is:
Fa1=(μg−1)(R11−R21)(1)
Where Fa is the focal length in air, μg is the refractive index of the glass (lens material), and R1,R2 are the radii of curvature of the lens surfaces.
2. Analyze the lens in liquid:
When the object and the lens are immersed in a liquid, a real image is formed, enlarged three times the object size.
-
Magnification M′=−3 (real and inverted image).
-
Let the new focal length in the liquid be Fl.
-
Let the object distance be u′ and the image distance be v′.
-
From magnification formula: M′=u′v′=−3. Since u′ is negative for a real object, v′ must be positive. So, v′=−3u′. (e.g., if u′=−x′, then v′=3x′).
-
Using the lens formula: v′1−u′1=Fl1
Substitute v′=−3u′:
−3u′1−u′1=Fl1
−3u′1−3=Fl1
−3u′−2=Fl1
3u′2=Fl1
So, u′=32Fl. (Note: Here u′ is used as the magnitude of object distance for simplicity in this step. If we stick to sign convention, u′=−32Fl and v′=2Fl).
Let's re-do this using u′=−x′ and v′=3x′ as in thought process.
3x′1−(−x′)1=Fl1
3x′1+x′1=Fl1
3x′1+3=Fl1
3x′4=Fl1⟹x′=34Fl.
-
The magnitude of the object distance is ∣u′∣=34Fl.
It is generally assumed that the object position relative to the lens remains the same unless specified otherwise. Therefore, we assume the object distance is the same in both cases:
∣u∣=∣u′∣
2Fa=34Fl
Fl=23Fa(2)
The lens maker's formula for a lens in liquid is:
Fl1=(μlμg−1)(R11−R21)(3)
Where μl is the refractive index of the liquid.
3. Calculate the refractive index of the liquid (μl):
Divide equation (3) by equation (1):
1/Fa1/Fl=(μg−1)(μlμg−1)
FlFa=(μg−1)(μlμg−1)
Substitute Fl=23Fa from (2) into this equation:
(3/2)FaFa=(μg−1)(μlμg−1)
32=(μg−1)(μl1.5−1)
Given μg=1.5.
32=(1.5−1)(μl1.5−1)
32=0.5(μl1.5−1)
Multiply both sides by 0.5:
0.5×32=μl1.5−1
31=μl1.5−1
Add 1 to both sides:
31+1=μl1.5
34=μl1.5
Now, solve for μl:
μl=1.5×43
μl=23×43
μl=89
The refractive index of the liquid is 89.
