Question

A convex lens has its radii of curvature equal. The focal length of the lens if $f$ . If it is divided vertically into two identical plano-convex lenses by cutting it, then the focal length of the plano-convex lens is:
[ $\mu$ - the refractive of the material of the lens]
A. $f$
B. $\dfrac{f}{2}$
C. $2f$
D. $\left( {\mu - 1} \right)f$

Answer 1

The initial focal length $f$ can be found in terms of radius of the curvature using the lens maker formula. When the lens is divided vertically, each identical plano-convex lens has two different radii now. The radius of the plane mirror is taken as infinite and we consider the value $\dfrac{1}{\infty } = 0$ . The focal length of both the plano-convex will be equal.

Complete step by step answer:
A convex lens consists of two radii; we are given that both the radius is equal. Let the radius be $R$ .
The refractive index of the lens is given as, $\mu$
Using lens maker formula, the focal length will be given as:
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_2}}} - \dfrac{1}{{{R_1}}}} \right]$ -equation $1$
Here, $\mu$ is the refractive index of the material of the lens.
But we are given that both the radius of the lens is equal, let the radius be $R$ :
$\Rightarrow {R_1} = {R_2} = R$
We know that the radius of convex lens has opposite direction, let ${R_1} = - R$ and ${R_2} = R$
Substituting this value in the lens maker formula, we get
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{R} - \dfrac{1}{{\left( { - R} \right)}}} \right]$
$\Rightarrow \dfrac{1}{f} = \dfrac{{2\left( {\mu - 1} \right)}}{R}$
$\Rightarrow \dfrac{1}{f} = 2 \times \dfrac{{\left( {\mu - 1} \right)}}{R}$
$\Rightarrow \dfrac{1}{{2f}} = \dfrac{{\left( {\mu - 1} \right)}}{R}$ --equation $2$
When the lens is divided vertically, it forms two identical plano-convex lenses as shown below:

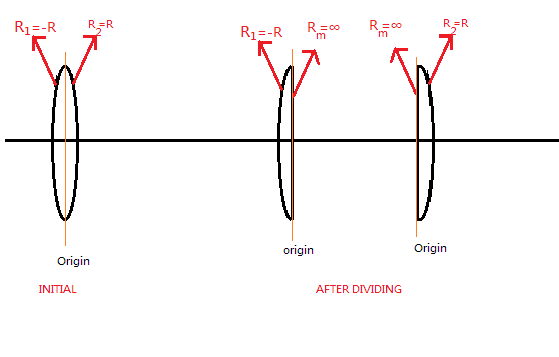
Applying lens maker formula for plano-convex mirror with radius ${R_1}$ , we get
$\dfrac{1}{{{f_o}}} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_m}}}} \right]$
Here, ${R_m}$ is the radius of plane surface, the radius of plane mirror is ${R_m} = \infty$ and we have ${R_1} = - R$ , ${f_o}$ is the focal length of the divided plano-convex lens.
Substituting these values in above equation, we get
$\dfrac{1}{{{f_0}}} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{ - R}} - \dfrac{1}{\infty }} \right]$
$\Rightarrow \dfrac{1}{{{f_0}}} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{ - R}} - 0} \right]$ as $\dfrac{1}{\infty } = 0$
$\Rightarrow \dfrac{1}{{{f_0}}} = \dfrac{{\left( {\mu - 1} \right)}}{{ - R}}$
Taking magnitude only, we have:
$\Rightarrow \dfrac{1}{{{f_0}}} = \dfrac{{\left( {\mu - 1} \right)}}{R}$
But from equation $2$ , we have
$\dfrac{1}{{2f}} = \dfrac{{\left( {\mu - 1} \right)}}{R}$
$\Rightarrow \dfrac{1}{{{f_0}}} = \dfrac{1}{{2f}}$
$\Rightarrow {f_0} = 2f$
Therefore, the focal length of the plano-convex lens will be $2f$

So, the correct answer is “Option A”.

Note:
For convex lenses, one of the radii is taken as positive and the other is taken as negative.
The radius of the plane mirror is infinite.
From the result it is observed that when a convex lens of equal radius is divided vertically its focal length is doubled.
When the lens is divided vertically, each identical plano-convex lens has two different radii now.